<Topic>
• Learning Theory
- Underfitting and Overfitting
- Addressing Overfitting
- Bias-Variance Problem
• Introduction to Deep Learning: Image Classification
- Training Deep Neural Networks
- Loss Function
- Derivative of Neural Networks
- Stochastic Gradient Descent (SGD)
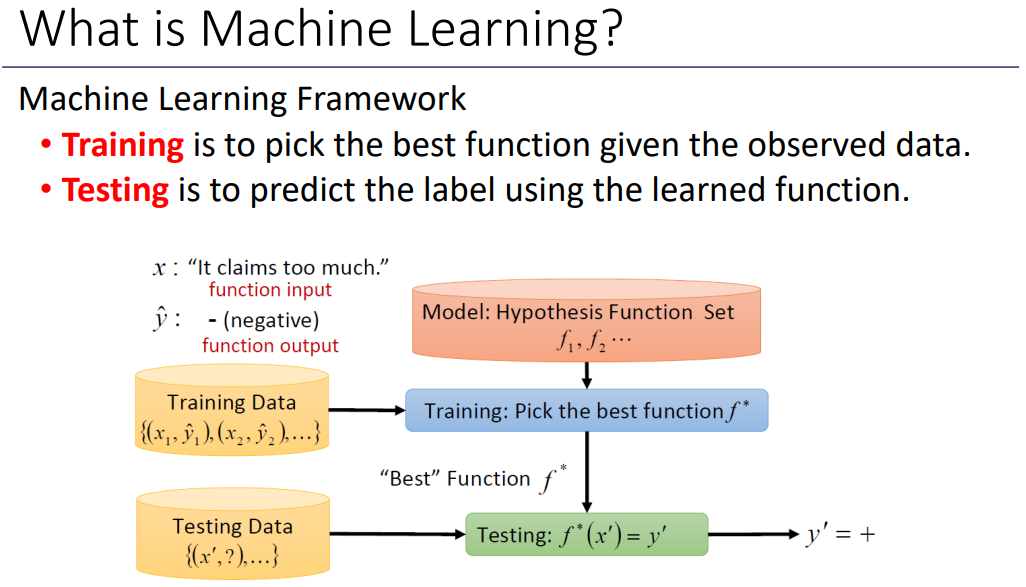
Training은 관찰된 데이터가 주어진 최상의 기능을 선택하는 것이고, Testing은 학습된 함수를 사용하여 라벨을 예측하는 것으로 쉽게 말하면 인풋을 통해 아웃풋을 찾는 과정이다.
1.1 Underfitting and Overfitting
모델이 너무 제한적이거나 너무 풍부할 수 있다.
Underfitting은 모델이 충분한 설명을 할 수 없는 현상이고, Overfitting은 모든 데이터에 fitting이 되는 것을 찾으려 하다 보니 새로운 인풋들이 들어왔을 때, generation이 잘 되지 않는 문제가 발생한 현상이다.
Underfitting과 Overfitting 모두 바람직하지 않은 현상이다.
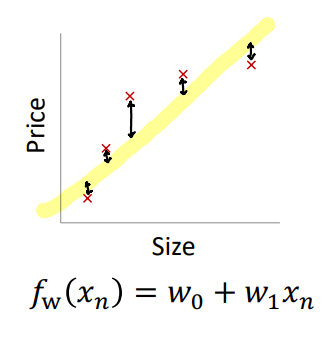
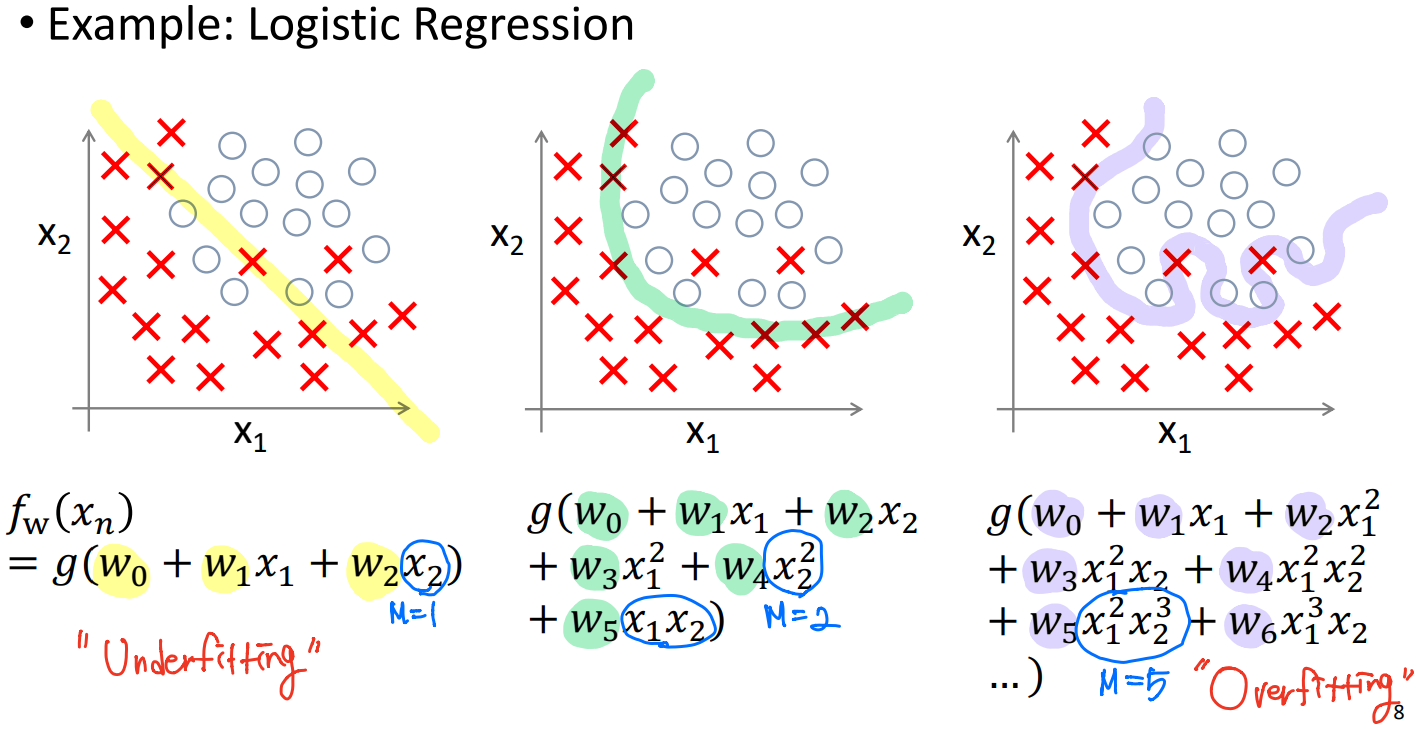
위는 주택 가격을 예측하는 Regression 예제이다. (선형 모델에 대한 Underfitting)
실제로 데이터가 linear하지 않은데, 우리는 linear한 모델을 찾으려 하기 때문에 에러가 발생한다. 이 때, 에러의 값은 en = yn - fw(xn) 으로 아웃풋과 모델의 아웃풋의 차이값이다.
결과적으로 위와 같이 데이터를 충분히 설명하지 못해 Underfitting 현상이 나타난다.
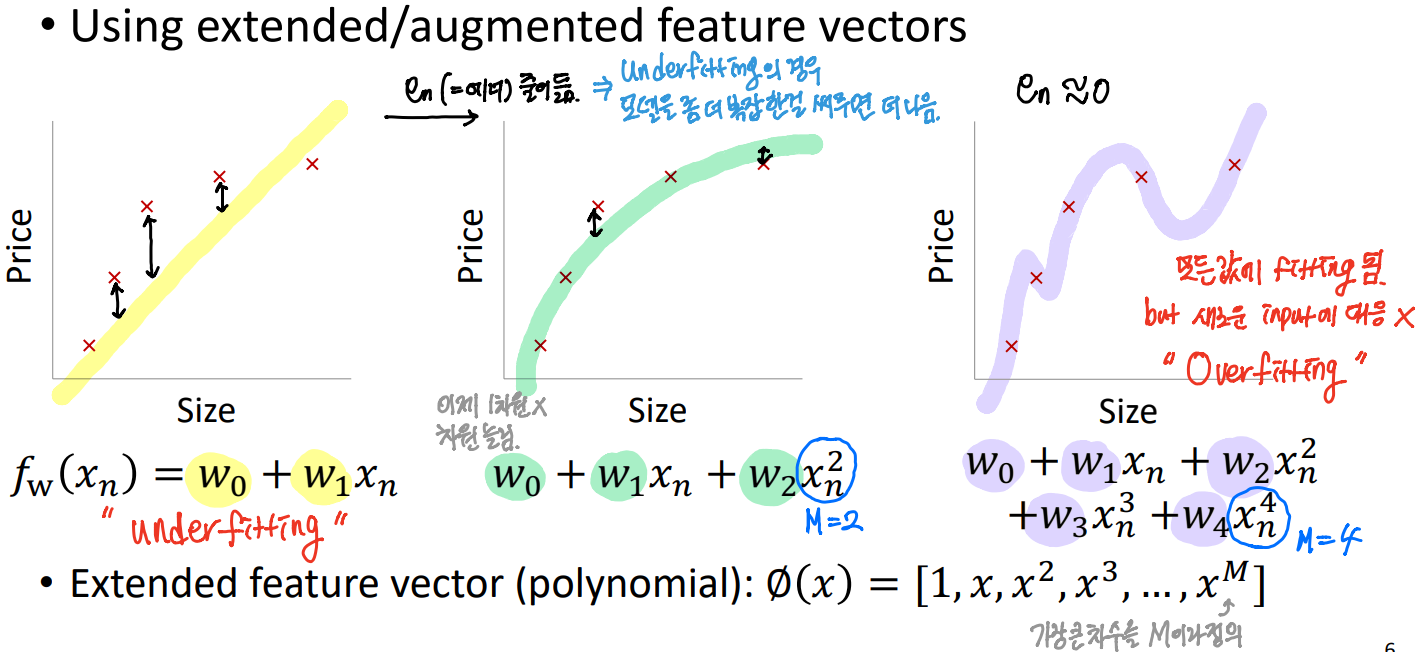
첫 번째 그래프는 Underfitting을 나타내고 있고, 가운데는 정상, 세 번째 그래프는 모든 값에 fitting이 되지만 새로운 인풋에 대해 대응하지 못하기 때문에 Overfitting의 모습을 나타낸다.
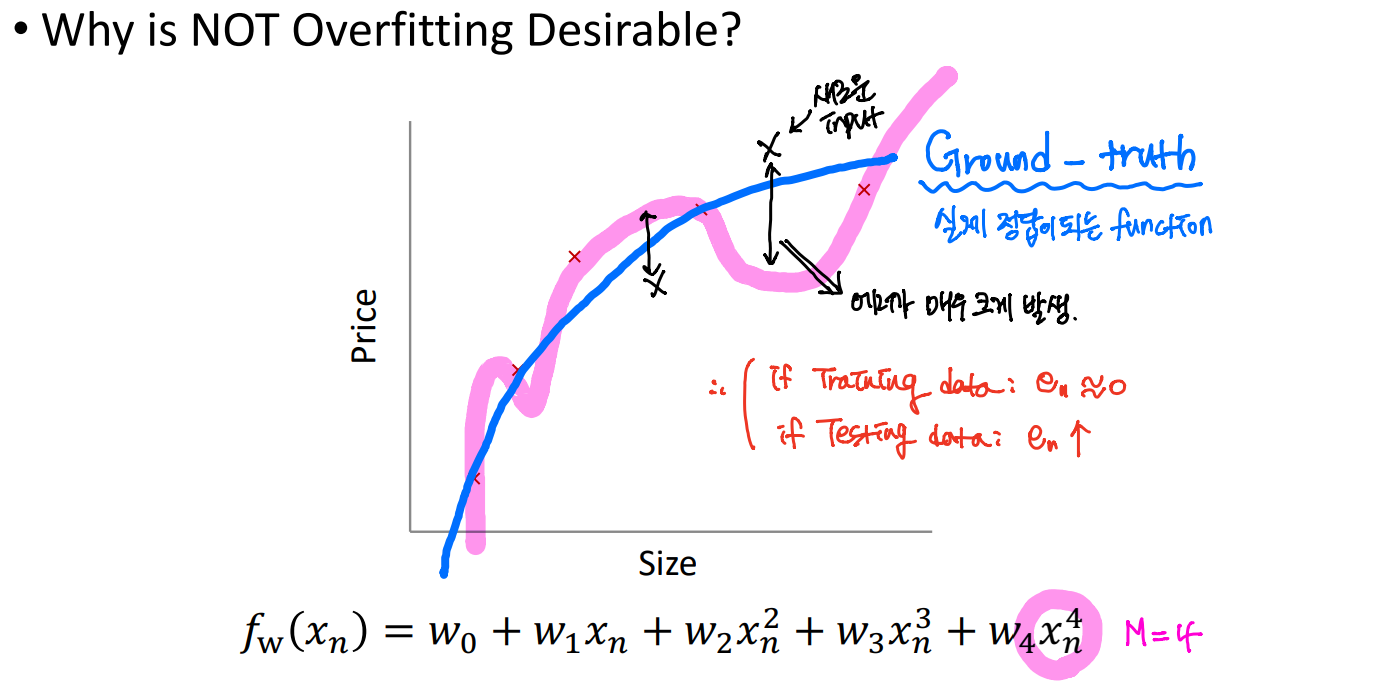
1.2 Adressing Overfitting
Overfitting을 해결하는 방법은 다음과 같다.
① 더 많은 training 데이터
② Regularization
- 모든 feature는 유지하면서 크기는 줄인다. => 너무 data에 Overfitting되는 문제를 줄일 수 있다.
- y를 예측하는 여러 feature들이 있을 때 각각 잘 작동한다.
③ feature의 number/degree 감소(즉, 단순한 모델)
- 보관할 feature을 수동으로 선택한다.
- 모델 선택 알고리즘
1.2.1) More Data
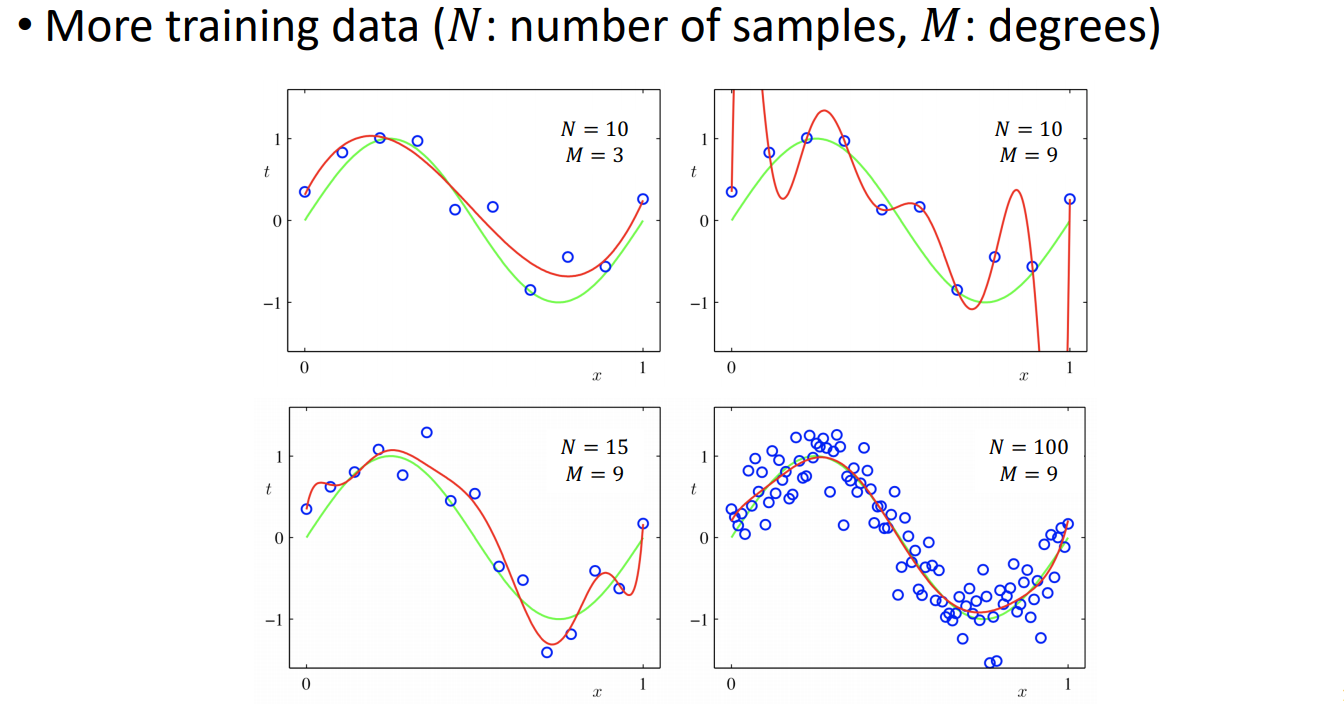
위 네 그래프에 그려져 있는 초록색 실선은 Ground-truth을 나타낸다. 우리는 이 Ground-truth과 비슷한 function을 찾는 것이 목표이다.
2번째 그래프를 보면, degree 값인 M이 커지게 되어, 너무 Overfitting되는 문제가 있다. 그리고 3번째 그래프를 보면 M의 값은 9로 그대로 두고 N의 값을 15로 키워서 Overfitting이 좀 줄어듦을 확인할 수 있다. 마지막으로 4번째 그래프를 보면 N=100으로 데이터의 수가 충분히 많은 경우, degree가 올라가도 Ground-truth과 유사한 function이 찾기 가능하다.
1.2.2) Regularization
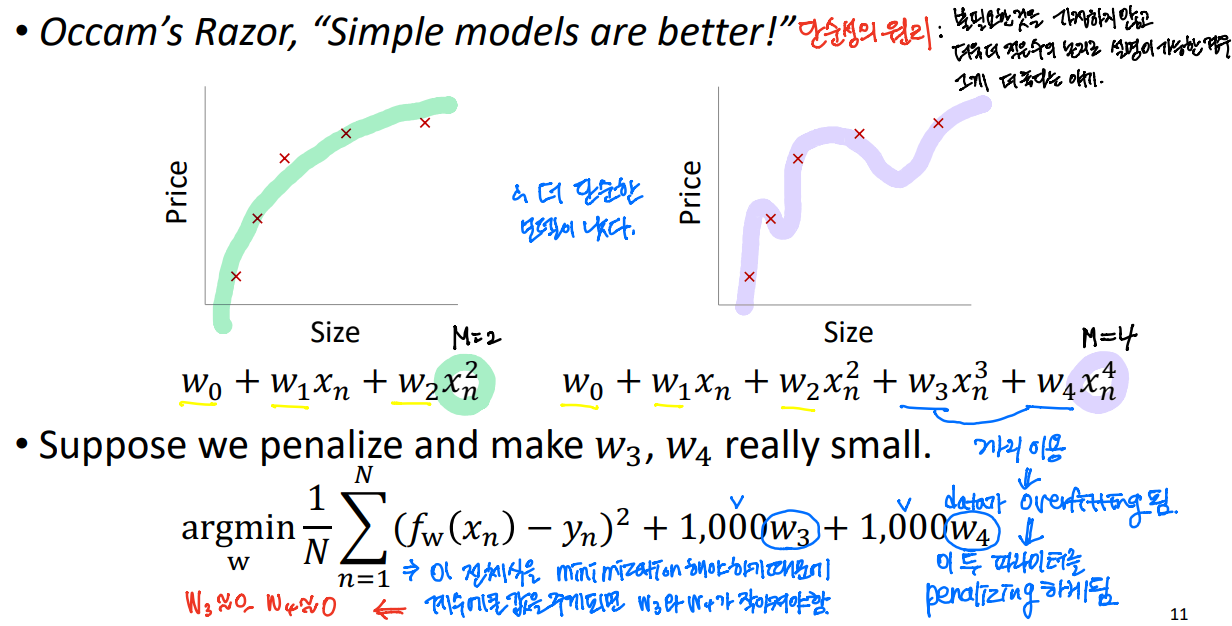
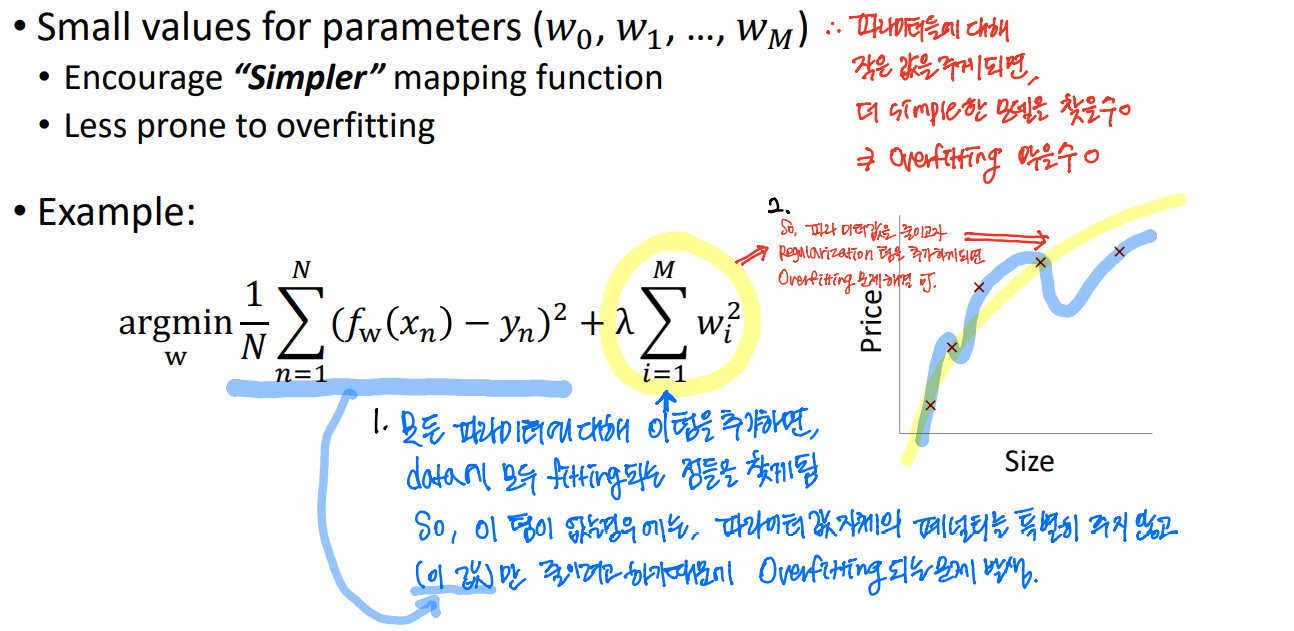
파라미터에 대해 작은 값을 주게 되면, 더 simple한 모델을 찾을 수 있다. => Overfitting을 막을 수 있다.
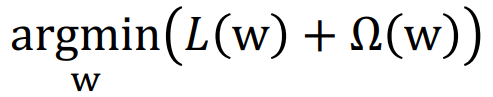
Regularization를 통해, 우리는 복잡한 모델에 불이익을 줄 수 있고 간단한 것을 선호한다.
regression을 하기 위해 Loss function을 minimization을 하는데, L(w)는 이 때, MSE 또는 MAE를 사용한다. 더불어 Ω(w)도regularization을 한다.
- Ω(w)는 레귤레이터로, 측정값은 w가 제공한 모델의 복잡성을 나타낸다.
- 작은 것은 괜찮지만 페널티를 적용했으니까 주요 영향은 대형 모델 wi이 받게 될 것이다. //보충
어떤 모델의 weight가 너무 커지는 것을 막아준다.
실제로는 어떤 feature term이 큰 지 알 수 없기 때문에 모든 w에 대해 regularization을 주게 된다.

가장 자주 사용되는 regularizer는 표준 유클리드 규범(L-2 norm)이다.
L(w)가 MSE일 때, 이를 Ridge Regression이라고 한다.
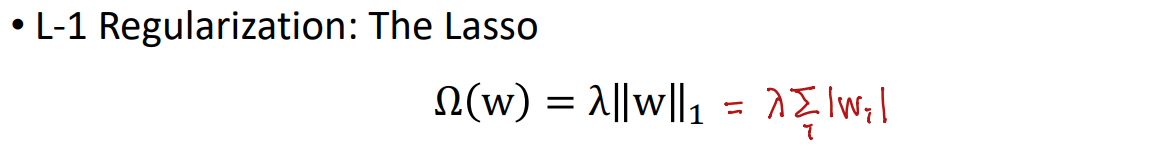
L-1 정규화를 위해, 최적의 솔루션은 L-2 정규화를 사용하는 경우에 비해 희소하다. (0이 아닌 구성 요소가 거의 없다)
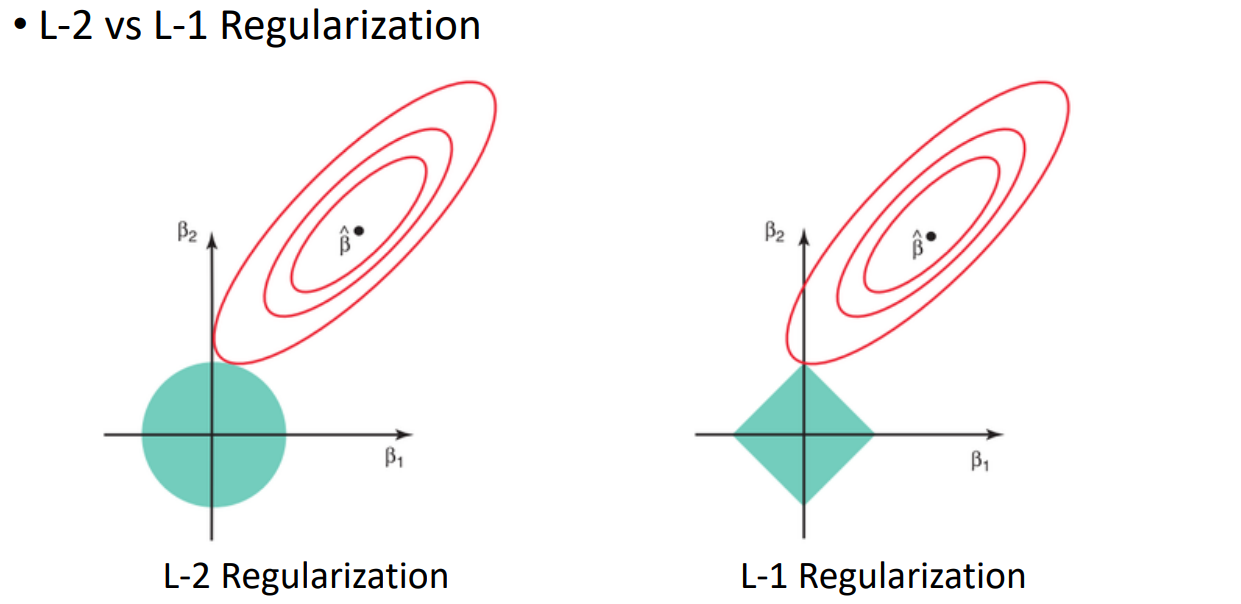
이 그래프에서 minimization하는 값은 β^ 이다. 우리는 이걸 찾으면 된다.
regularization을 줬기 때문에, 파라미터들의 L-2 norm이 최소화되어야한다. => 두 지점 β1과 β2가 만나는 곳이 최적의 좌표이다.
L-1 Regularization의 경우에는, L-1은 축위에 존재하기 때문에 L-2에 비해 좀 더 sparse한 점을 갖는다.
1.2.3) Model Selection
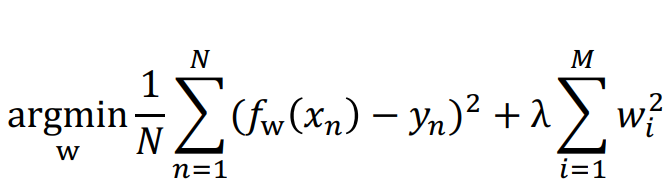
Ridge Regression에서는, 최소화할 대상 w를 위 식으로 선택한다.
그러면 우리는 모델의 성능을 어떻게 제어할 수 있을까?
• 모델 복잡성(ex. degree M in a polynomial feature)
• 페널티 파라미터 λ → 어느 정도만큼 Regression 시켜줄지를 나타냄
그러면 우리는 이러한 하이퍼파라미터(ex. M, λ, 등)를 어떻게 선택할까?
• Model Selection 문제
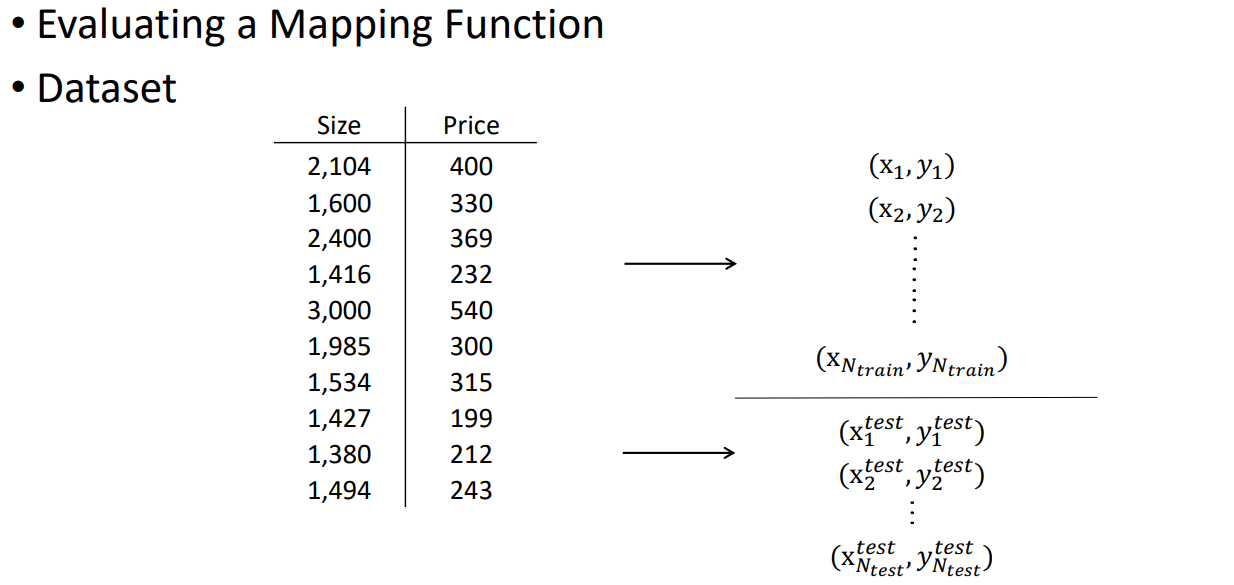
(x1, y1), (x2, y2), ~, (xNtrain, yNtrain) : Training phase
(x1^test, y1^test), (x2^test, y2^test), ~, (xNtrain^test, yNtrain^test) : Testing phase
(1) Linear Regression을 이용한 Training/Testing 절차는 다음과 같다.
• Triaing error를 최소화하여 Testing data에서 매개 변수 w를 학습한다.
• Testing sample들을 이용한 error 계산식은 아래 식과 같다. (이 때, testing sample들에 대해서만 error를 계산한다.)
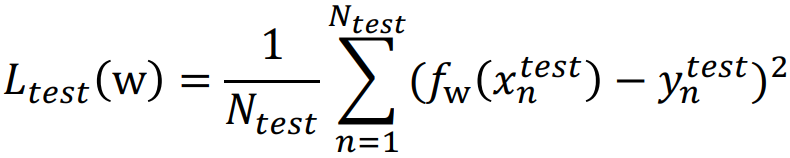
(2) Logistic Regression을 이용한 Training/Testing 절차는 다음과 같다.
• Triaing error를 최소화하여 Testing data에서 매개 변수 w를 학습한다.
• Testing sample들을 이용한 error 계산식은 아래 식과 같다.
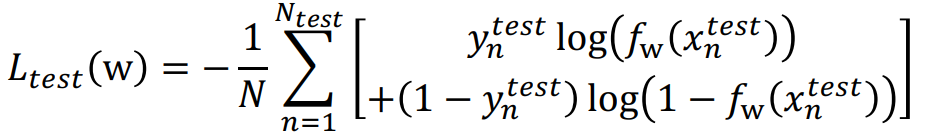
또는 misclassification error (0/1 misclassification error).

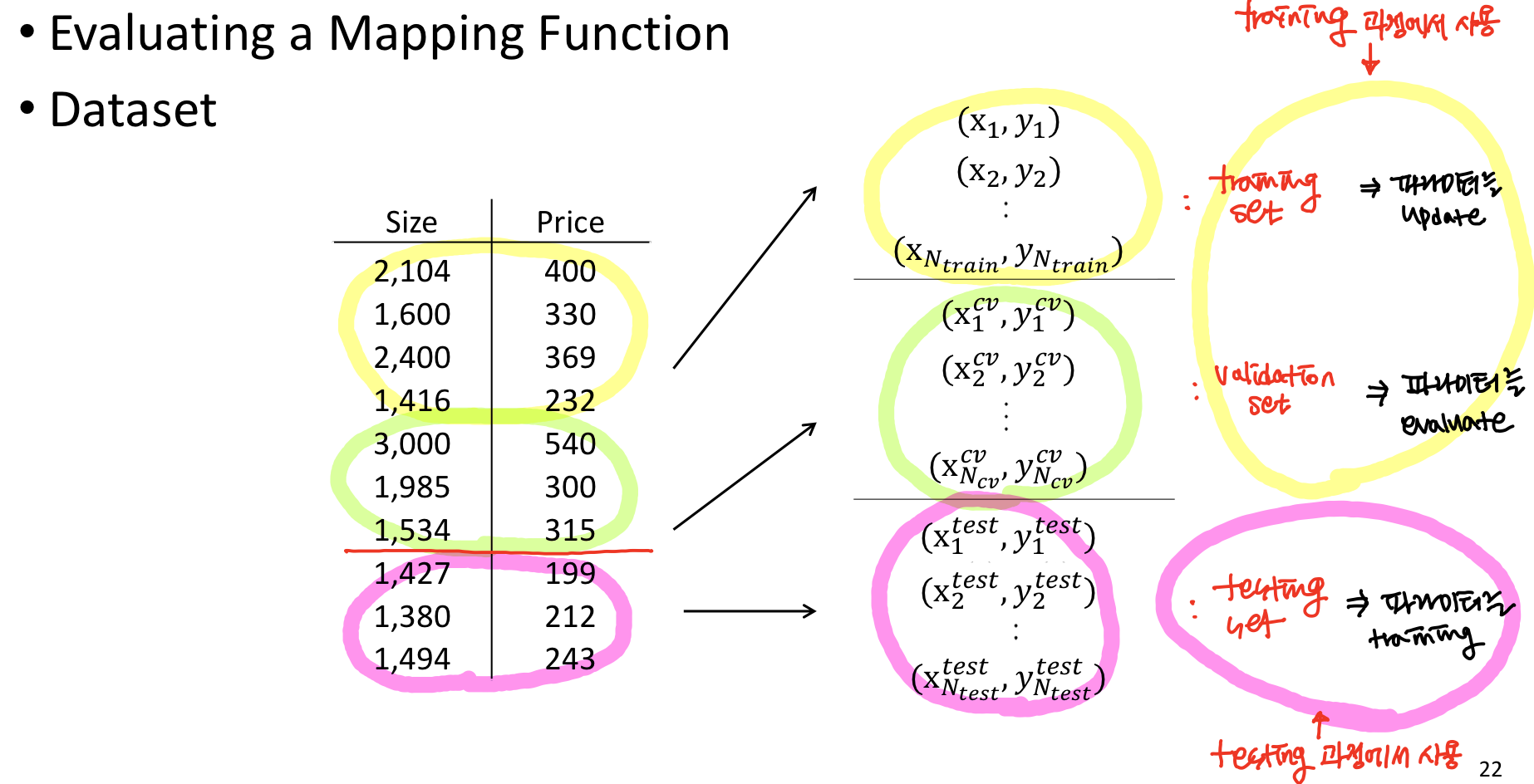
앞에서는 data를 training sample과 testing sample 이렇게 2가지로 나눴는데, training 과정을 통해 파라미터를 업데이트하고 testing 과정을 통해 testing을 했다. 하지만 실제로는 testing sample들은 training 과정에서는 사용 안되는 문제점들이 있기 때문에 위와 같이 validation set을 새롭게 정의한다.
위 예시는 training 과정에서 evaluation할 수 있도록 data를 임의로 줬다.
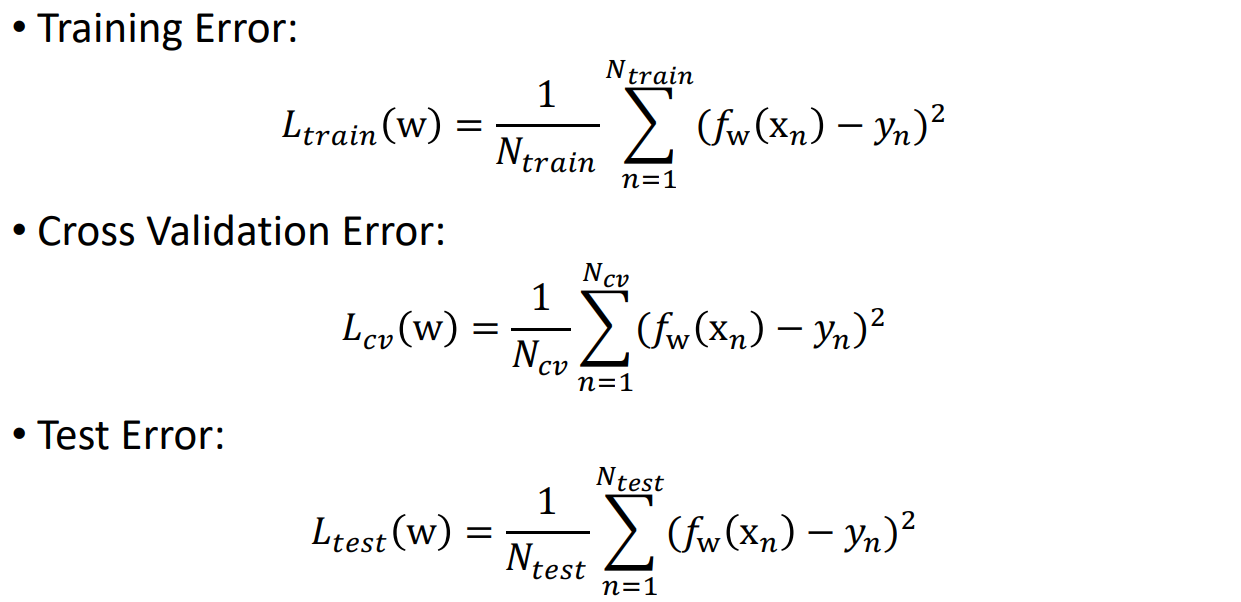
앞에서는 test set error를 계산했었다. 이제는 validation error를 계산해보자.
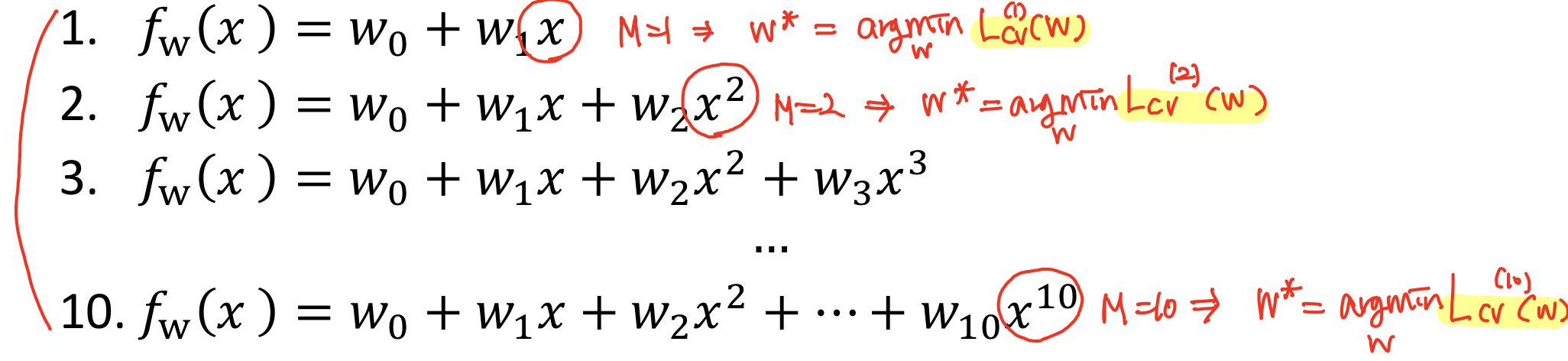
이 때 validation error가 가장 작았을 때의 것을 minimization 해주는 파라미터를 찾을 수 있다.
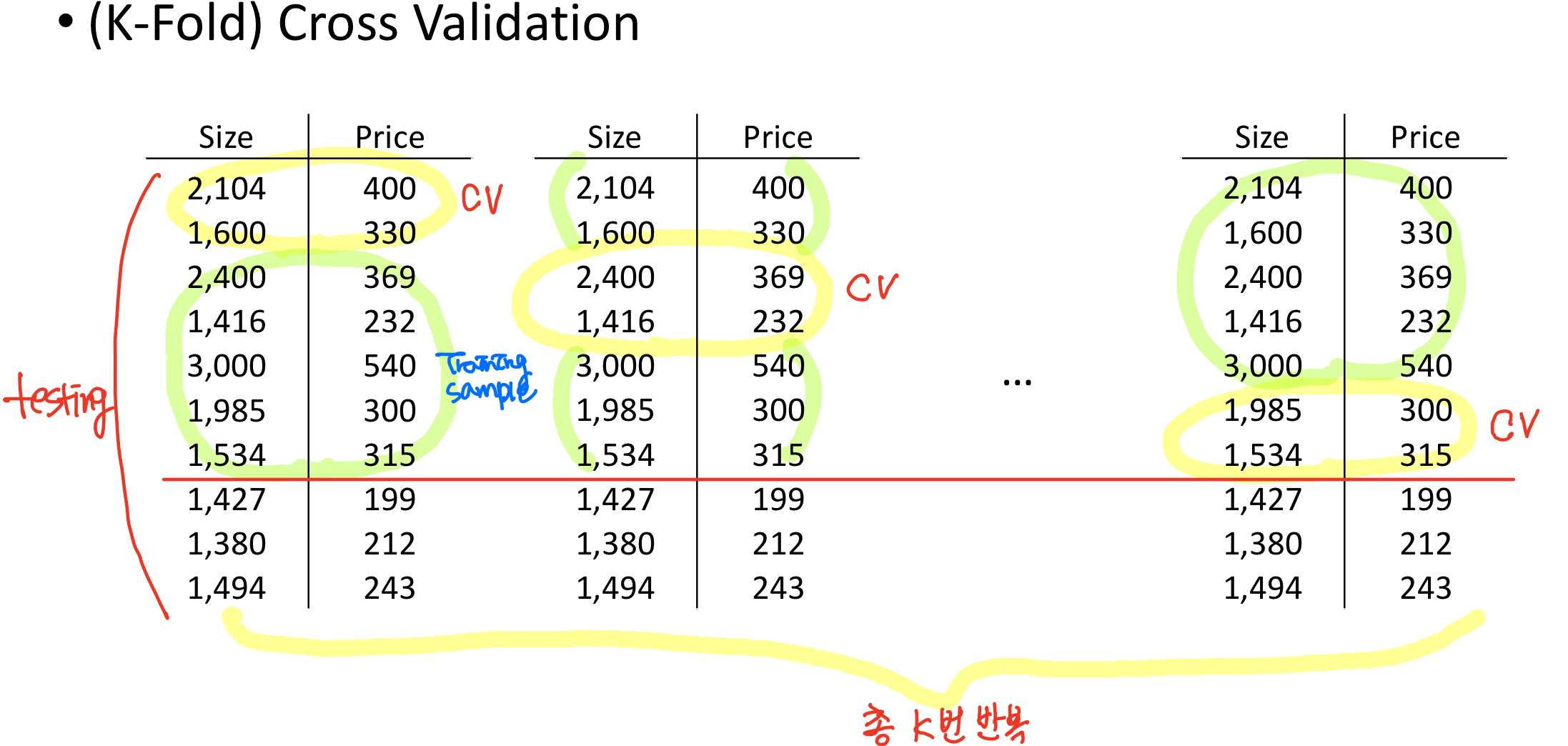
임의로 training set에서 샘플들을 training과 validatino sample들로 나눠서 학습을 할건데, 이게 고정되어 있으면 validation sample들이 항상 일정하고, training sample들만 이용해서 계속 업데이트하게 되기 때문에 모든 데이터를 효과적 이용이 불가능하다.
=> 그래서 K-Fold Cross Validation은 validation error를 k개로 나눠서 매번 다른 validation sample들을 갖고 파라미터를 evaluation한다.
∴ 매번 학습할 때마다 다른 training sample과 validation sample을 이용해서 모든 데이터가 골고루 사용될 수 있도록 한다.
1.3 Bias-Variance Problem
모델에서 에러가 발생했을 때, 2가지 원인을 Bias와 Variance로 구분지어 생각해볼 수 있다.
이 둘을 이해하면, 모델이 Underfitting 또는 Overfitting 되어서 적절하지 않다는 것을 분석하는데에 용이하다.
• Bias으로 인한 error: model의 예상(또는 평균) 예측과 우리가 예측하려는 실제 값 사이의 차이로 간주된다. (어떤 prediction을 한 결과가 실제값과 얼마나 차이를 발생시키는지.)
• Variance으로 인한 오차: 주어진 데이터 점에 대한 모형 예측의 변동성으로 간주된다. (어떤 모델을 prediction했을 때, 그것이 얼마나 큰 분포가 되어있는지.)
이러한 두 가지 유형의 error를 이해하면 모델 결과를 진단하고 과적합 또는 과소적합 실수를 방지하는 데 도움이 될 수 있다.
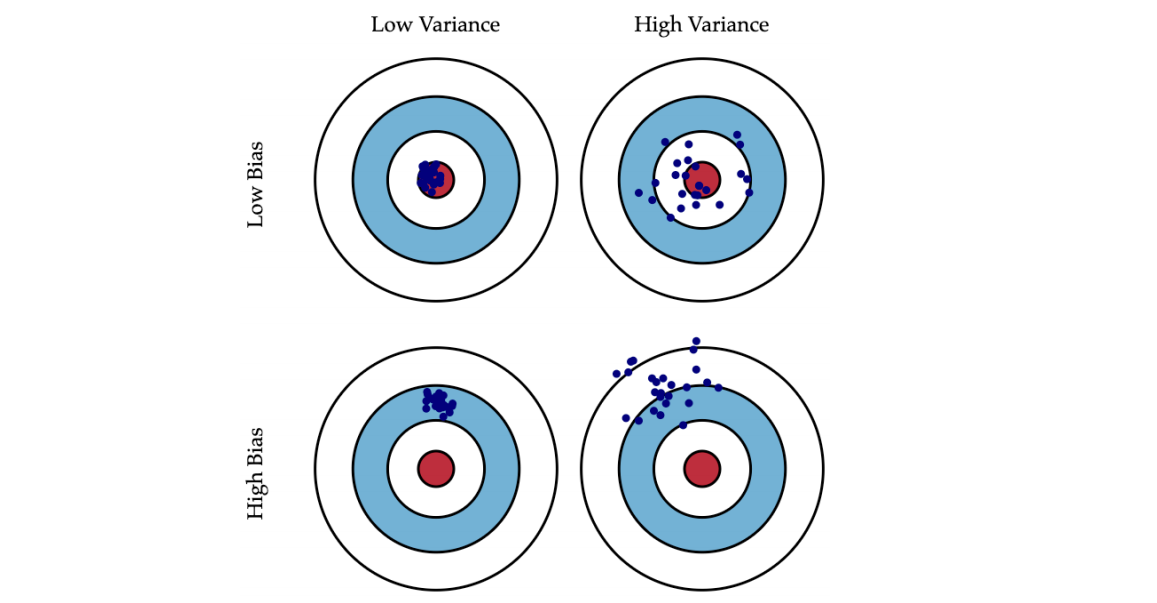
먼저 가운데 빨간색으로 채워진 동그란 원이 Ground-truth에 해당한다고 생각하자.
우리는 이것과 가깝기를 바라면서 가장 가까운 값을 예측할 수 있도록 모델을 찾게된다.
첫 번째 그림은 Low Bias, Low Variance이다.
Variance 값이 작기 때문에 분포가 작다. 그리고 Bias 값도 작기 때문에 Ground-truth과의 차이가 작은 부분에 몰려있다.
그리고 그 아래 그림은 High Bias, Low Variance이다.
Bias 값이 늘어났기 때문에, Ground-truth과의 거리가 늘어났다.
Low Bias, High Variance인 그림은 점의 분포가 크다.
여기서 Ground-truth과의 거리가 멀어지면 마지막 그림인 High Bias, High Variance에 해당한다.
=> 우리가 실제로 찾고 싶은 모델은 Low Bias, Low Variance이다.
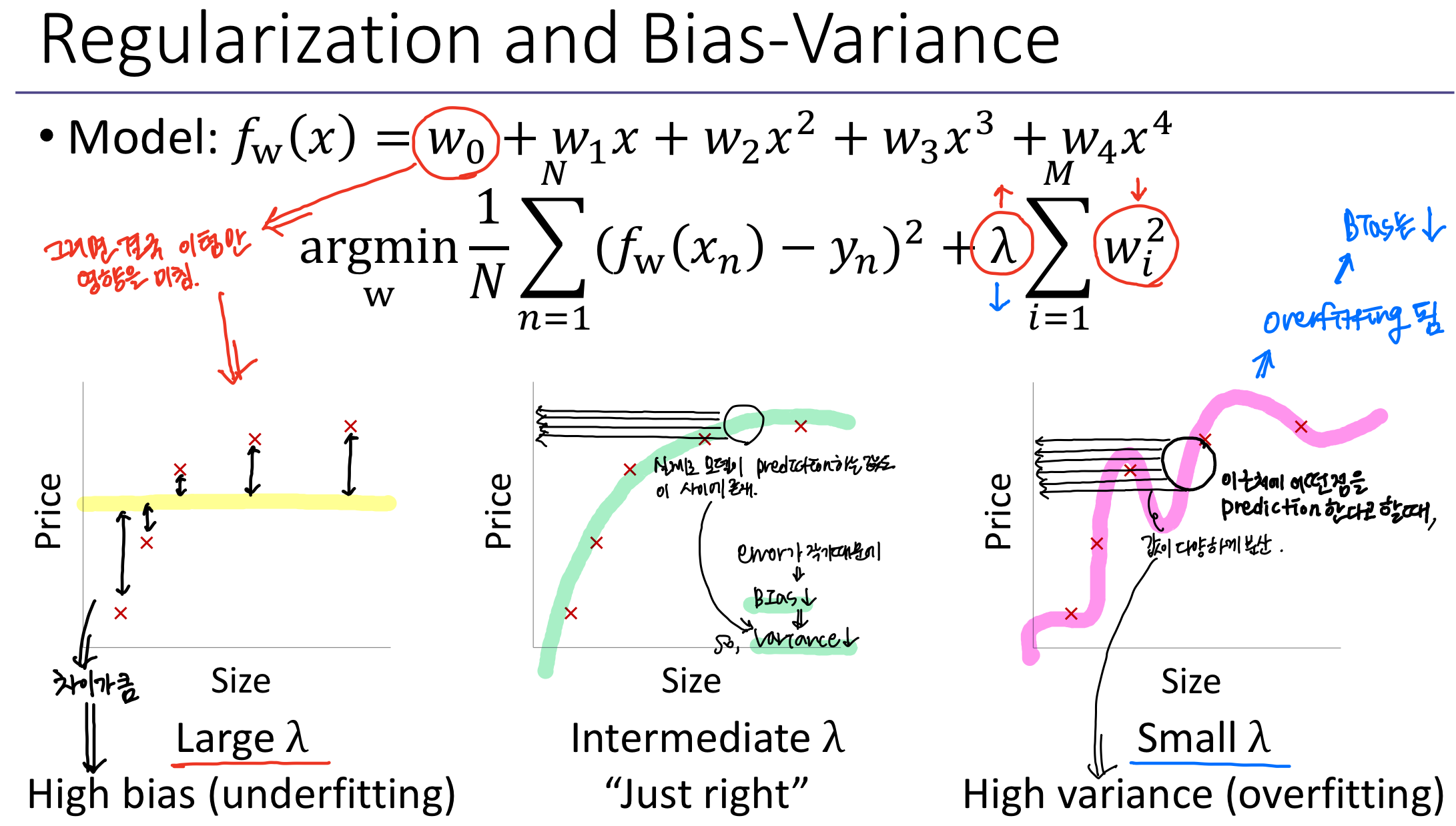
이제는 Regularization 관점에서 알아보자.
λ가 크면 -> w가 차지하는 값이 크기 때문에, 이걸 minimization해야하기 때문에 w가 작아져야한다.
λ가 작으면 -> 모든 모델에 fitting이 되는 w를 찾는다.
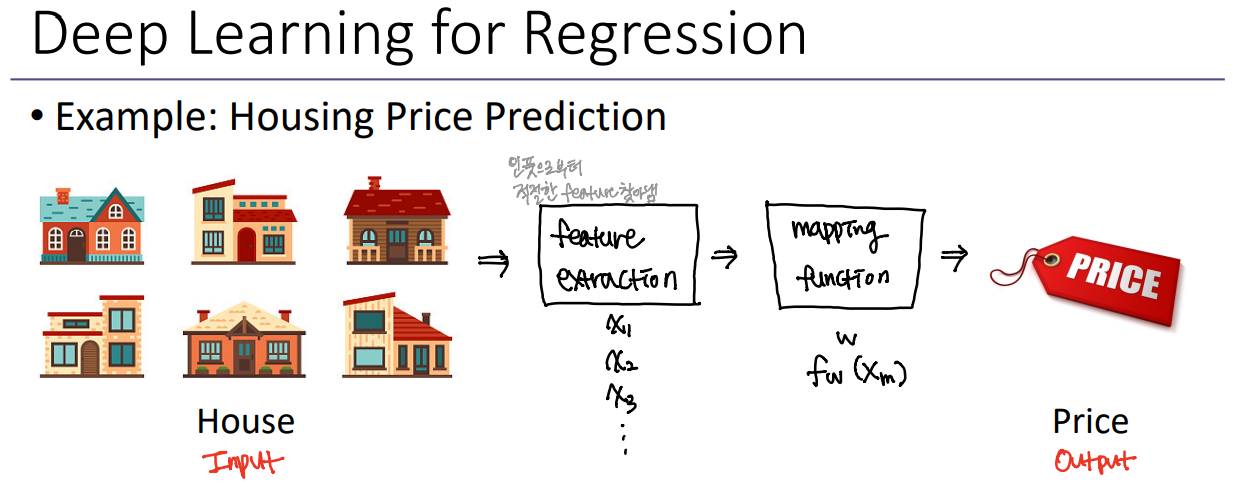
사실 딥러닝을 이용하면, 어떤 feature가 인풋과 아웃풋간의 관계를 잘 설명할 수 있는지 우리가 알 수 없다. 그래서 딥러닝에서는 feature extraction을 뉴럴 네트워크를 이용해서 최적의 feature를 자동적으로 네트워크상에서 찾아내고 이것을 이용하여 mapping functino을 이용해 인풋과 아웃풋간의 관계를 설명한다.
2.1 Training Deep Neural Networks
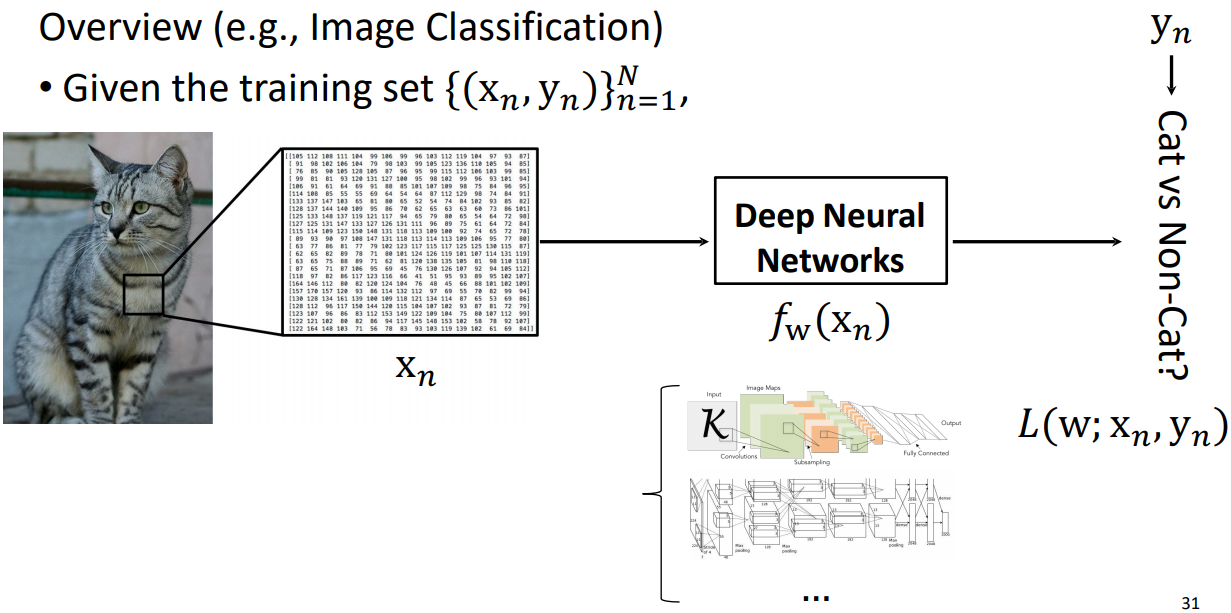
xn은 인풋이고 fw(xn)은 mapping function에 해당한다. yn은 cato인지 아닌지 구분하는 아웃풋이다.mapping function을 찾는 과정에서 1) 적절한 loss function을 설계 2) 이 loss를 최소화하기 위해 다양한 트레이닝 방법들을 이용해서 학습 (ex. gradient descent) 3) 이런 방법들을 이용해서 gradient계산해주고 파라미터를 최적화시켜서 매핑함수를 찾을 수 있게 된다.
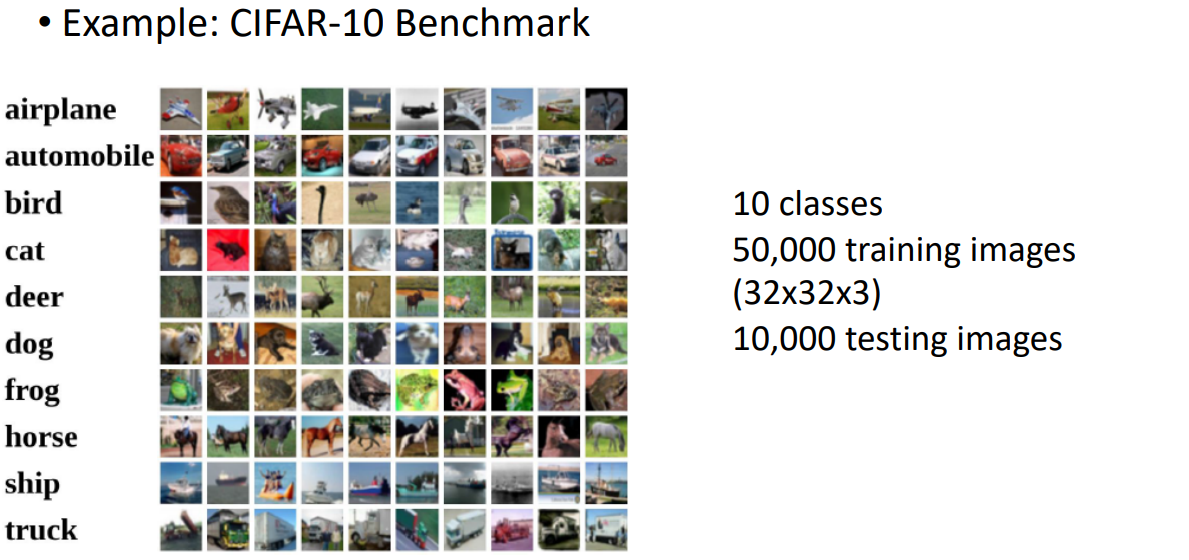
10 classes를 찾기 위해 50,000개의 training images ( (32x32x3) <- H(높이)xW(너비)xC(채널) 채널은 RGB, 3개의 채널이므로 3 )를 이용하고 10,000개의 testing images를 이용한다.
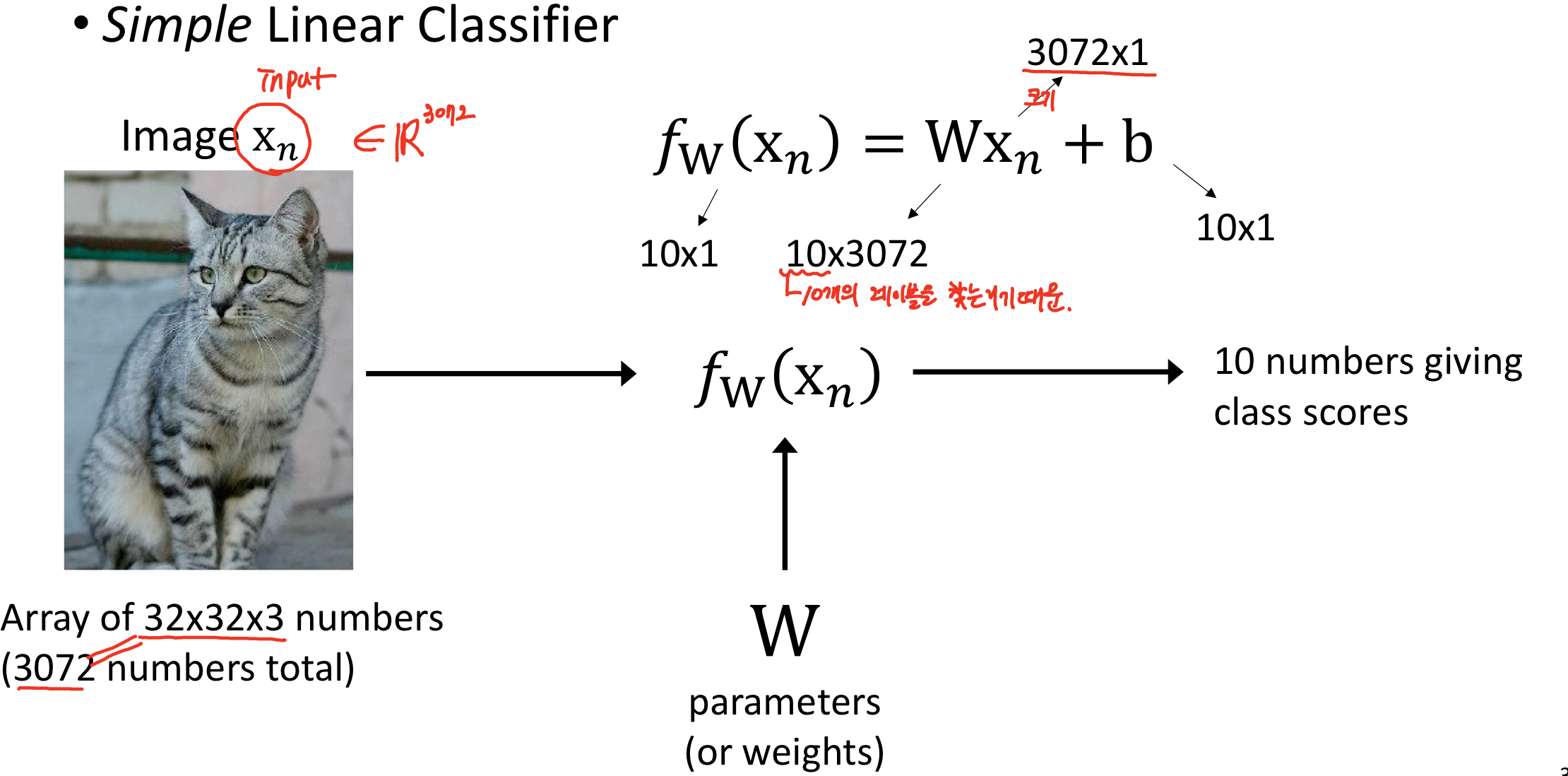
10개의 class 중, 어디의 class에 가장 높은 확률로 이 영상이 존재하는지를 찾는 과정이 easy? classification이다. //보충
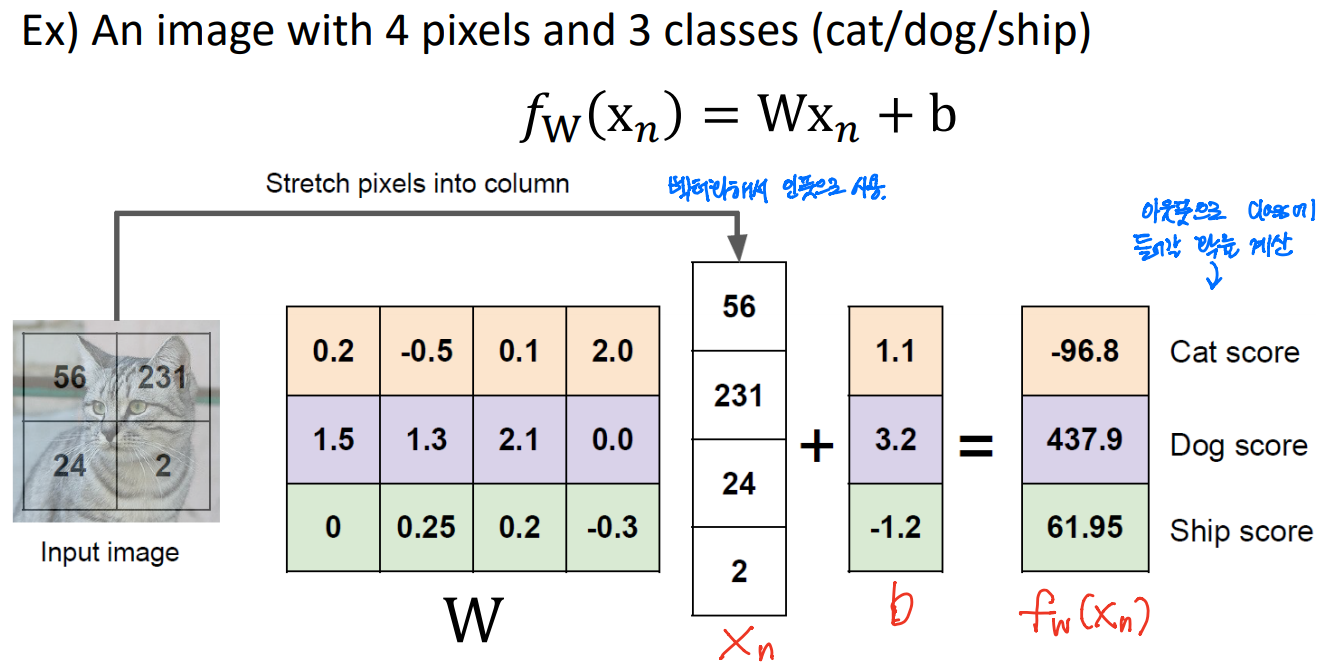
인풋 이미지를 벡터화하여 인풋으로 사용한다. 그리고 아웃풋으로 clss에 들어갈 확률을 계산한다.
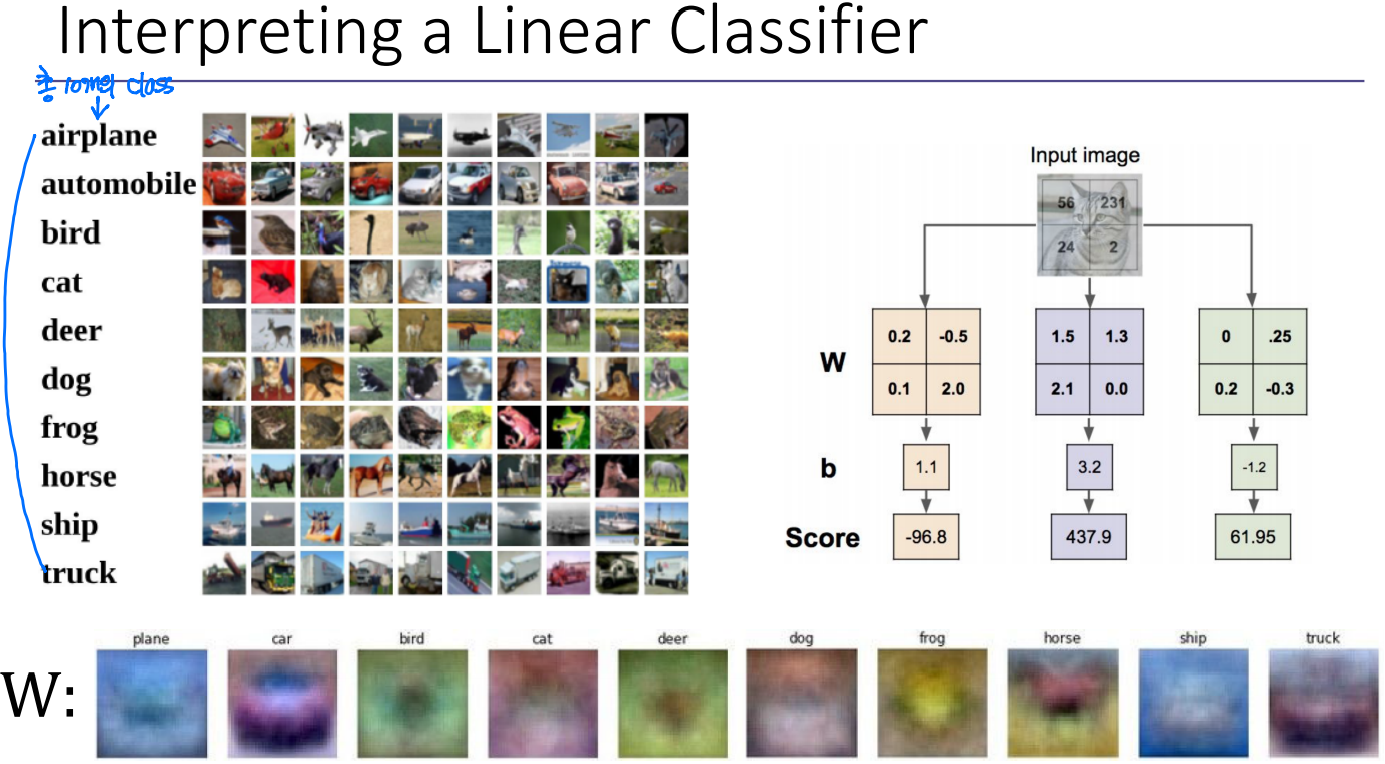
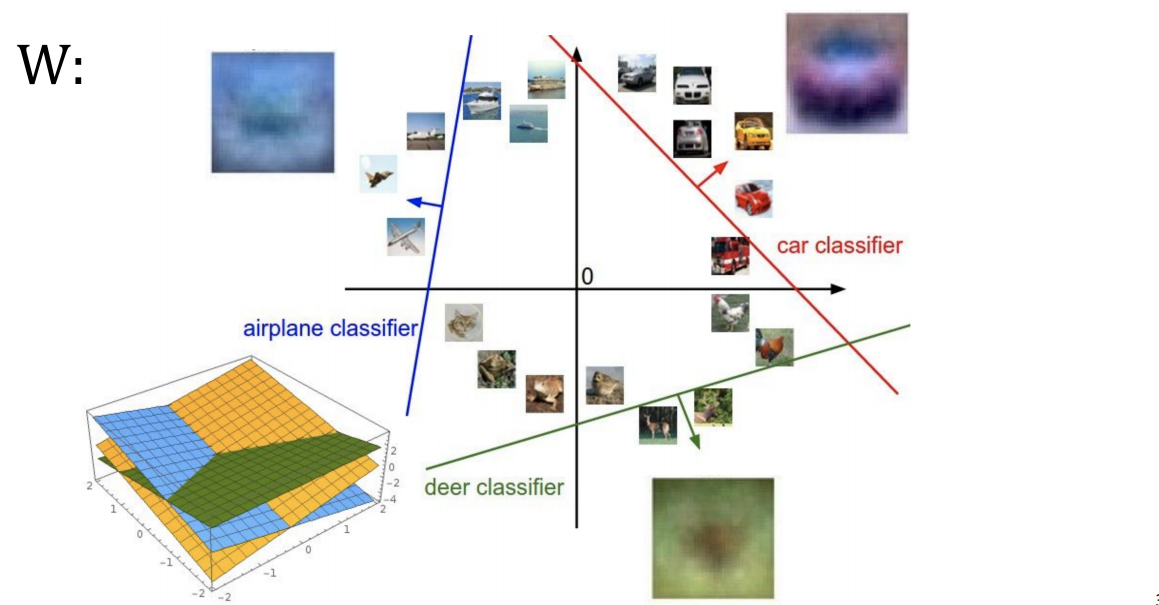
W를 찾는다는 것은 이 영상을 분리해낼 수 있는 decision boundary를 찾는다는 것이다.

이 W가 좋은지 나쁜지 어떻게 알 수 있을까? W를 찾기 위해서는,1) Loss function("좋은" W가 있다는 것이 무엇을 의미하는지 수량화)2) Optimization(random W부터 시작하여 loss를 최소화하는 W 찾기)위 예시에서는 3개의 영상을 인풋으로 줬다.
2.2 Loss Functions (or Cost Functions)
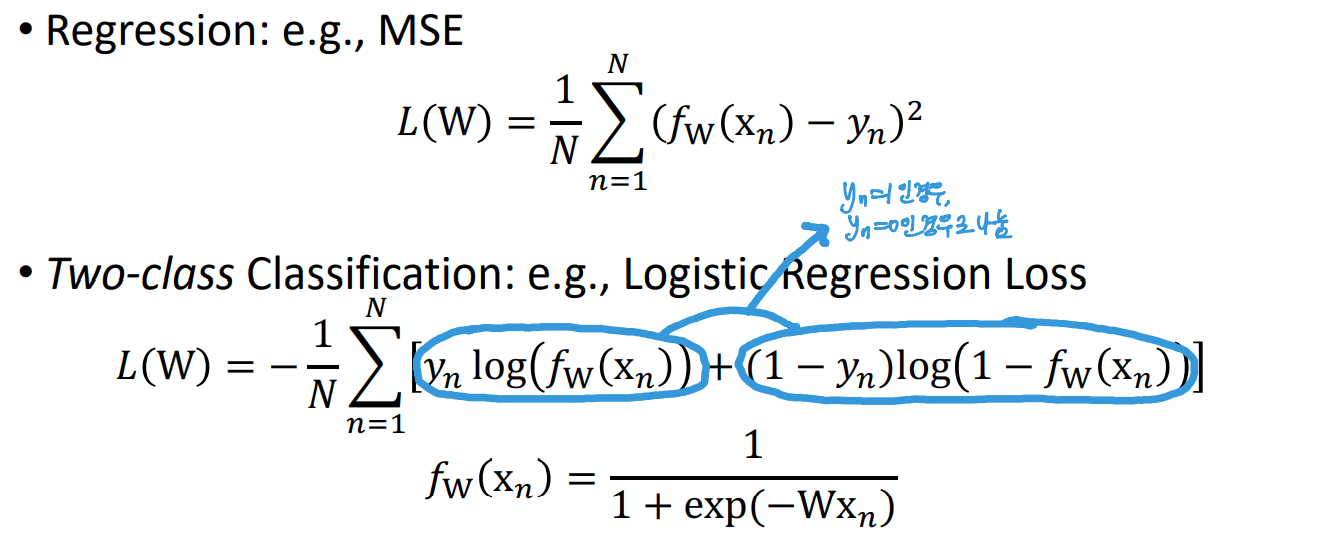


Multi-class Classification의 경우, 앞에서 확률의 형태로 각 원소가 0,1사이의 값을 가지고, 모든 원소의 합이 1이 되는 확률의 형태를 취하게 되고, 그것을 Log Likelihood Loss를 줘서 설계를 할 수 있다.어떤 벡터를 확률의 형태로 만들어주는 것을 소프트맥스 함수라 한다.그리고 Log Likelihood Loss를 이용해서 1일때는 cost가 0이 되고, 확률이 0에 가까우면 coss가 높아지는 형태로 Loss를 준다.

2.3 Derivative of Neural Networks

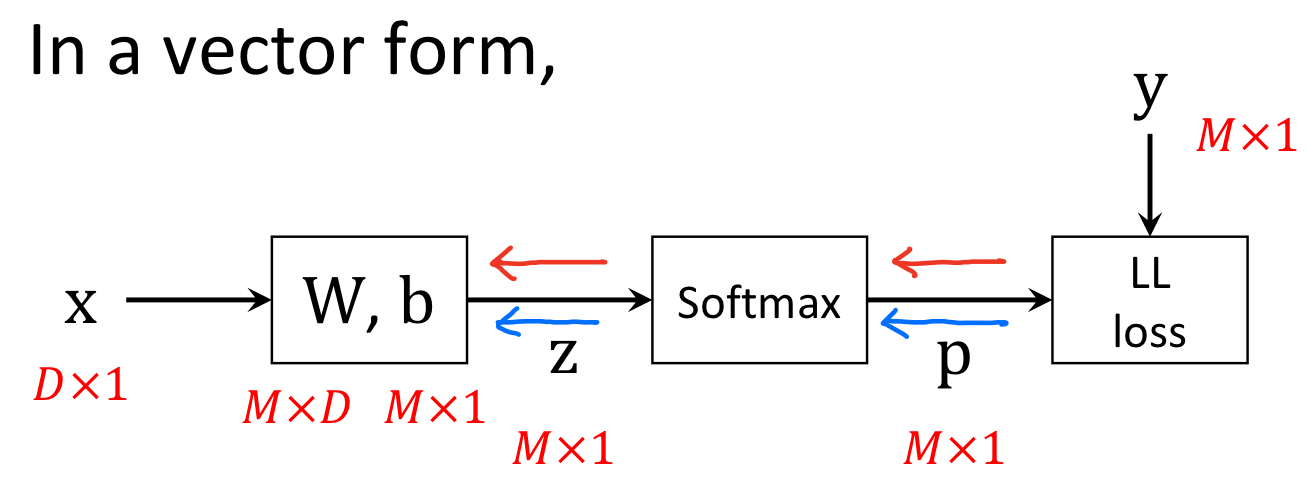
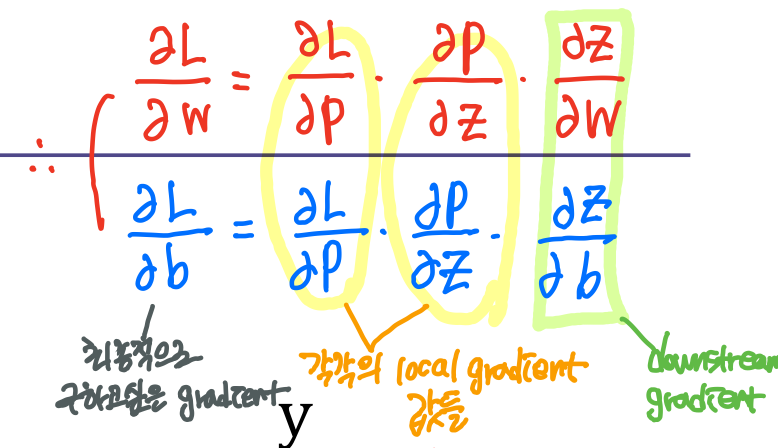



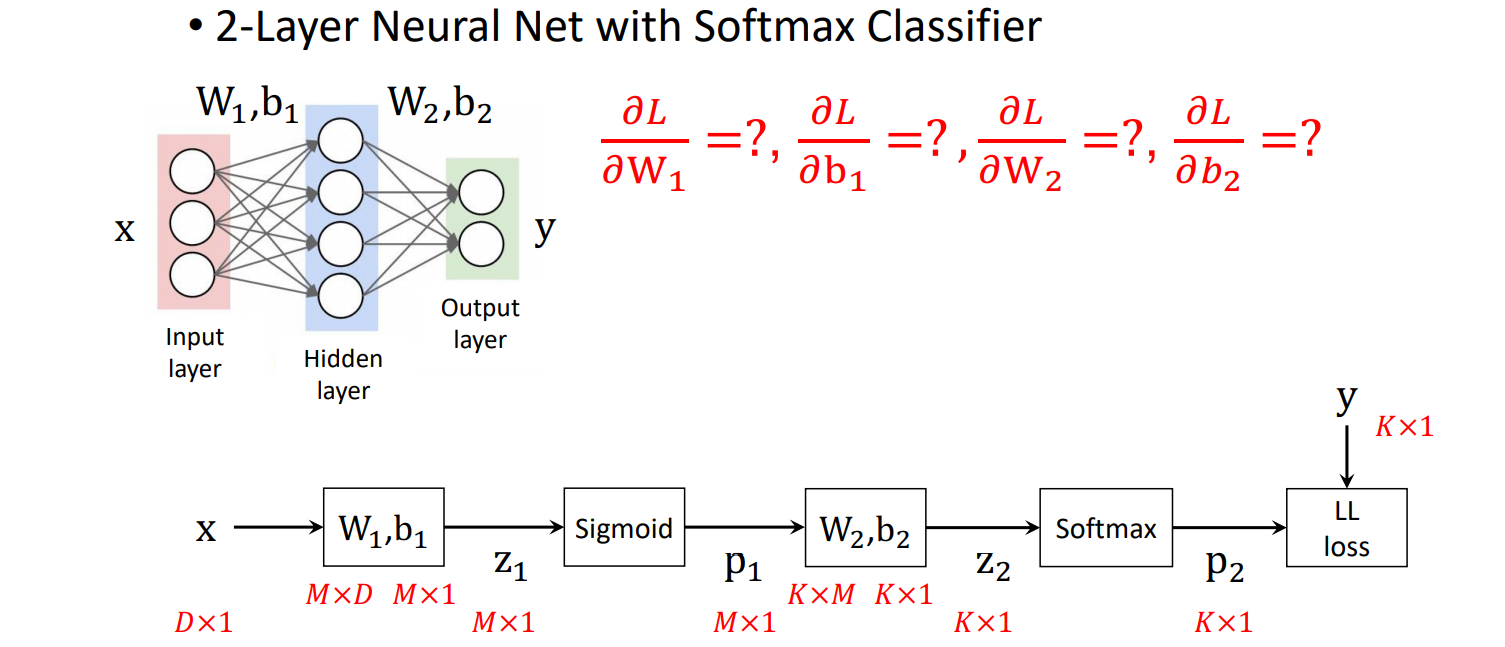
2.4 Stochastic Gradient Descent (SGD)
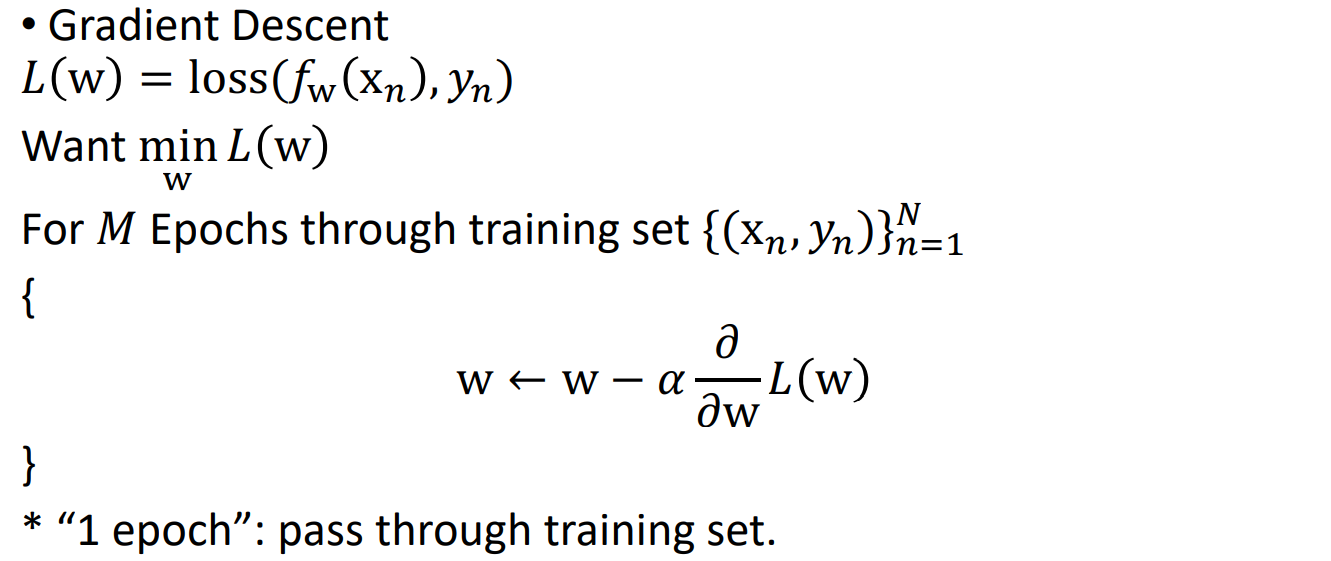
어떤 loss가 주어질 때 이 loss를 minimization하는 w를 찾는게 목표이다.n개의 트레이닝 데이터가 있을 때, 이 n개를 모두 통과해서 파라미터를 업데이트한다. 이때 n개의 training set를 한번 패스할 때를 1 epoch이라 한다. 모든 데이터를 다 통과해야 파라미터를 한번 통과하게 된다. 그래서 n이 커지면 계산량이 많아지는 문제가 있다. 해결책은 training sample들을 임의로 나누어서 32/64/128개로 나누어서, 그 mini batch 안에서 계산해서 해결한다. 이러한 방법을 Stochastic Gradient Descent라 한다.

Q. Gradient Descent와 Stochastic Gradient Descent의 가장 큰 차이점은 무엇일까?
=> Gradient Descent는 파라미터를 한 번 업데이트하기 위해서 전체 n개의 데이터를 모두 통과했을 때 파라미터를 한 번 업데이트한다. 이에 반해 Stochastic Gradient Descent는 training sample들을 mini batch로 나누고, 그 batch를 b개의 batch로 나누어서
batch를 한번 통과할 때마다 파라미터를 업데이트하도록 학습한다.
Gradient Descent와 비교했을 때의 장점은 총 계산량이 작아지기때문에 조금 더 계산 빨라진다.
그리고 gpu를 이용한 병렬 컴퓨팅이 가능해져서 계산속도 매우 향상된다.
Gradient 를 조금 더 샘플들을 이용해서 계산하기때문에 좀 더 정확하다.
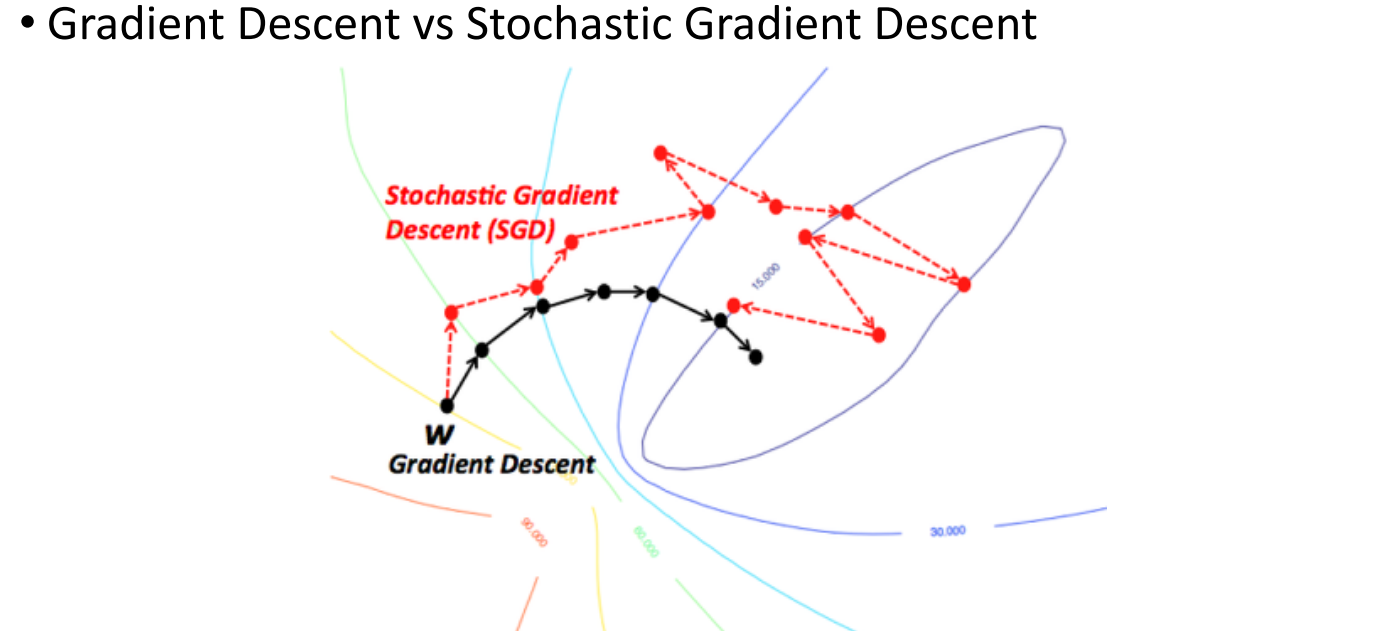
그림으로 비교해보자면, Gradient Descent는 최적의 해를 찾기 위해 모든 데이터를 이용하여 파라미터를 한 번씩 업데이트한다.이에 반해 Stochastic Gradient Descent는 임의의 샘플들을 잘게 쪼개어서 하기 때문에 좀 더 불안정하기는 하지만, 계산속도가 올라가고 그래디언트가 좀 더 정확하게 계산되고 수렴속도도 빨라진다.
'전공 > 컴퓨터 비전' 카테고리의 다른 글
| [컴퓨터 비전] Neural Networks and Backpropagation (0) | 2021.04.18 |
|---|---|
| [컴퓨터 비전] Linear Regression and Logistic Regression (0) | 2021.04.14 |
| [컴퓨터 비전] Introduction to Image Processing (2) | 2021.04.07 |
