<TOPIC>
• The Perceptron
• Neural Network Representation
• Computational Graph Representation
• Derivative of Neural Network
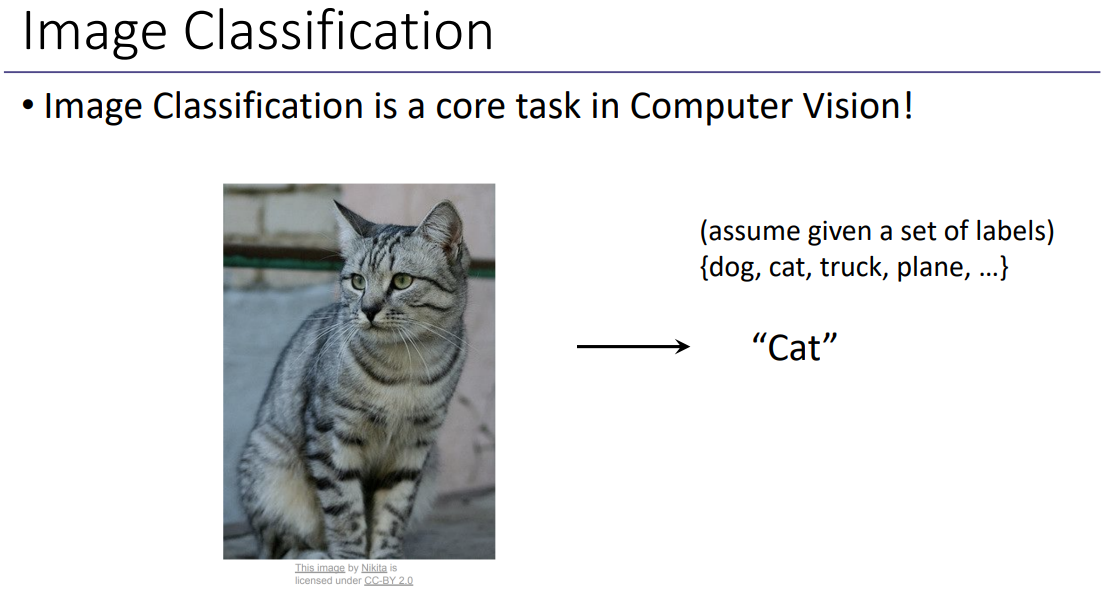
왼쪽의 고양이 이미지가 어떤 label에 속하는지 보는 작업이다.

Image classification의 어려운 점들은 위와 같이 여러가지가 있다. 먼저, 고양이의 몸통과 배경의 색이 비슷하여 인식이 어려운 경우가 있다. 그리고 조명의 변화에 따라서도 인식하기가 어려울 수 있고 신체 일부가 가려짐으로써 구별하기 어려울 수 있다. 또한 대상이 여러마리로 같이 있을 경우에도 인식하기 어렵다.
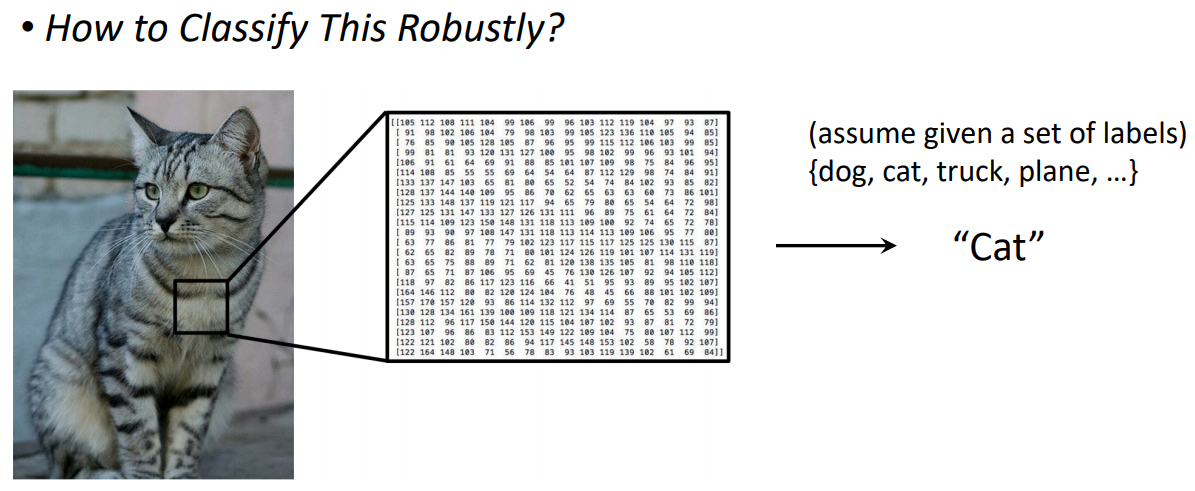
위와 같이 이미지는 픽셀값으로 구성되어있다.
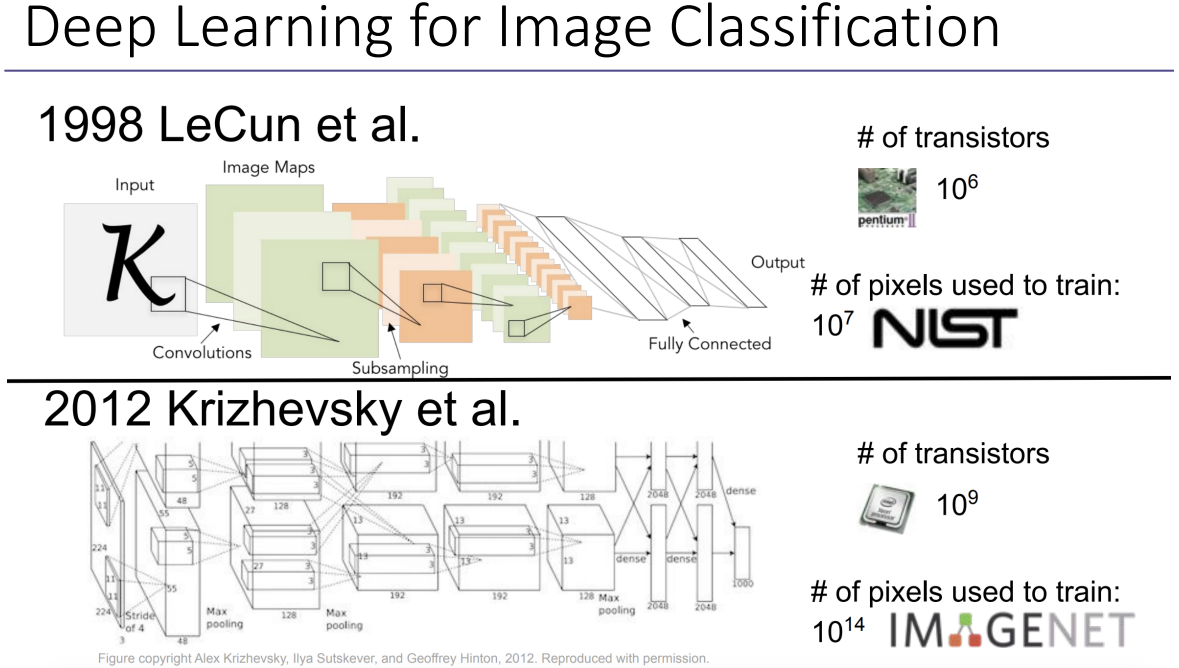
1998년 LeCun은 컨볼루션을 반복 수행하여 아웃풋을 도출한다. (위 사진에서 'Convolutions'이라고 표현된 것은 저번 공부에서는 필터링이라고 이해한 바 있다.) 이 때 사용되는 트랜지스터 파라미터의 개수는 10^6개이고 이 네트워크를 학습시키기 위해 사용한 픽셀의 수는 10^7개이다.
2012년 Krizhevsky에서 사용된 트랜지스터 파라미터의 개수는 10^9개이고 네트워크를 학습시키기 이ㅜ해 사용된 픽셀의 수는 10^14개이다.

빅데이터가 등장함에 따라 딥러닝을 이용한 image classification이 가능해졌다.
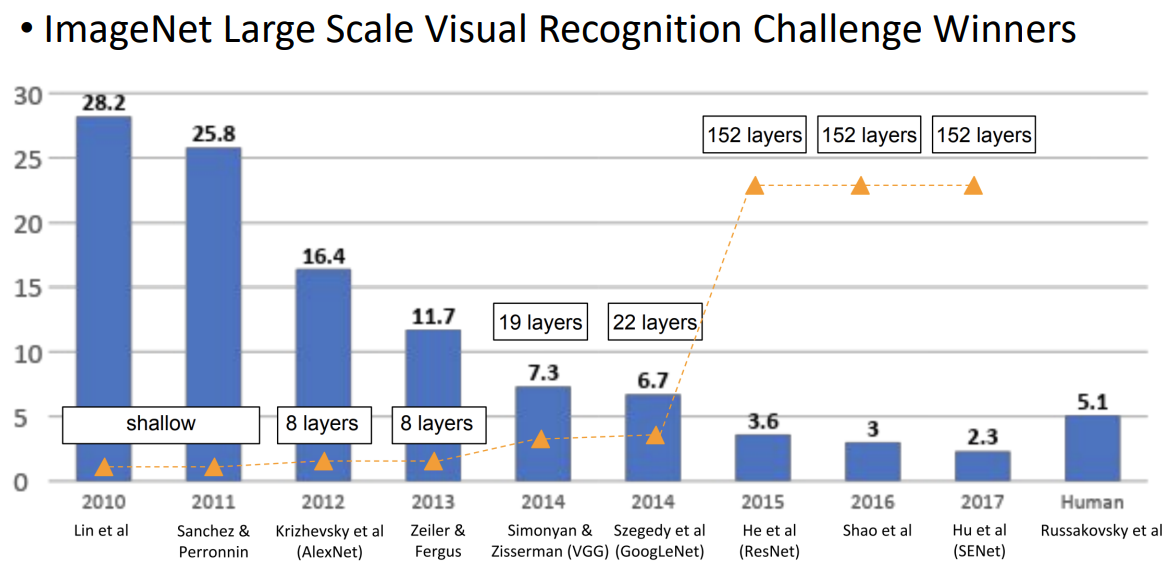
위 그래프에서 나타내는 y값 수치는 error를 의미한다. 2011년에서 2012년으로 가면서 AlexNet을 통해 에러 값이 굉장히 낮아짐으로써 정확도가 상승했다. 2014년에서 2015년으로 가면서는 layer의 수를 높이면서 정확도를 높일 수 있었다.
1. The Perceptron
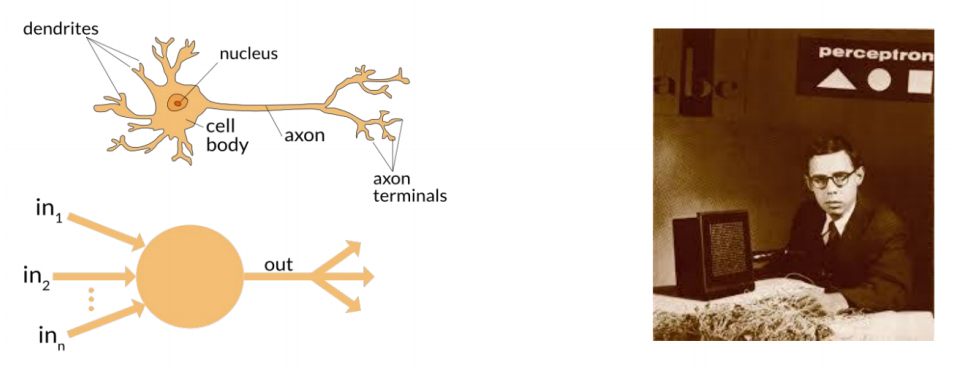
Perceptron(신경망)은 1958년 Frank Rosenblatt에 의해 신경생물학에서 영감을 받아 발명되었다.
신경생물학을 간단히 이해해보자면, 위 사진을 보면 dendrites(순상돌기)로부터 자극을 받아들여서 nucleus(핵)으로 전달된다. 그리고 axon(축삭)을 통해 이동하여 전달되고 axon terminals로 감으로써 신호를 만들어낸다.
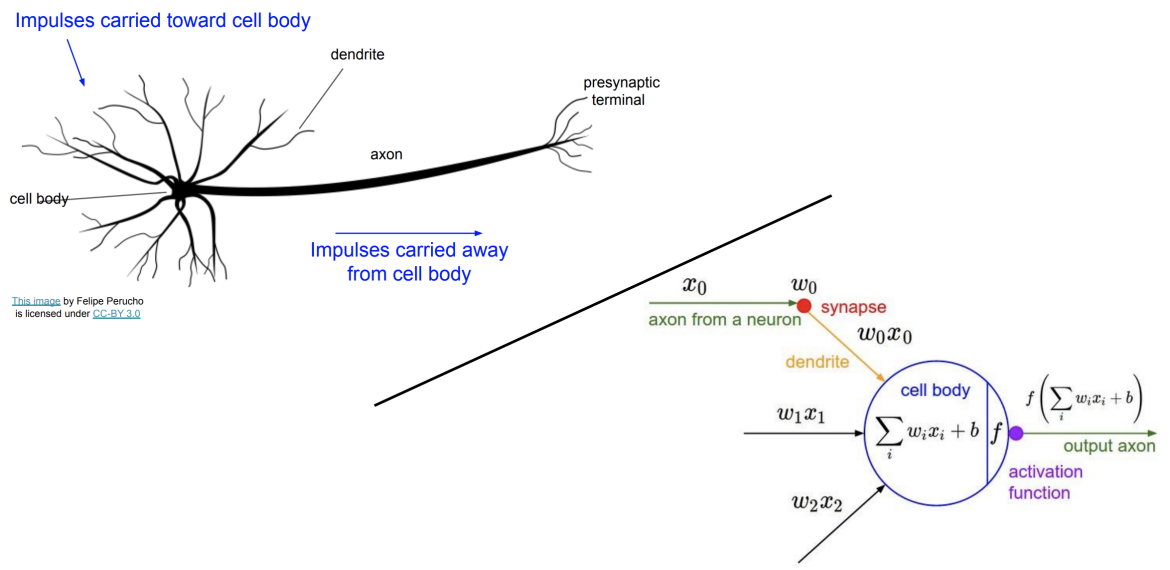
외부로부터 세포체로 전달될 자극이 들어오면 이 자극들은 axon을 통해 전달된다. 그리고 presynatic terminal에서 또 다른 신호를 만들어낸다. 이러한 기본 배경지식을 토대로 퍼셉트론을 이해하면, x0, x1, x2, ... xi는 인풋 값이다. 그리고 이 인풋들이 적절한 변환과정을 통해 아웃풋을 생성해낸다.
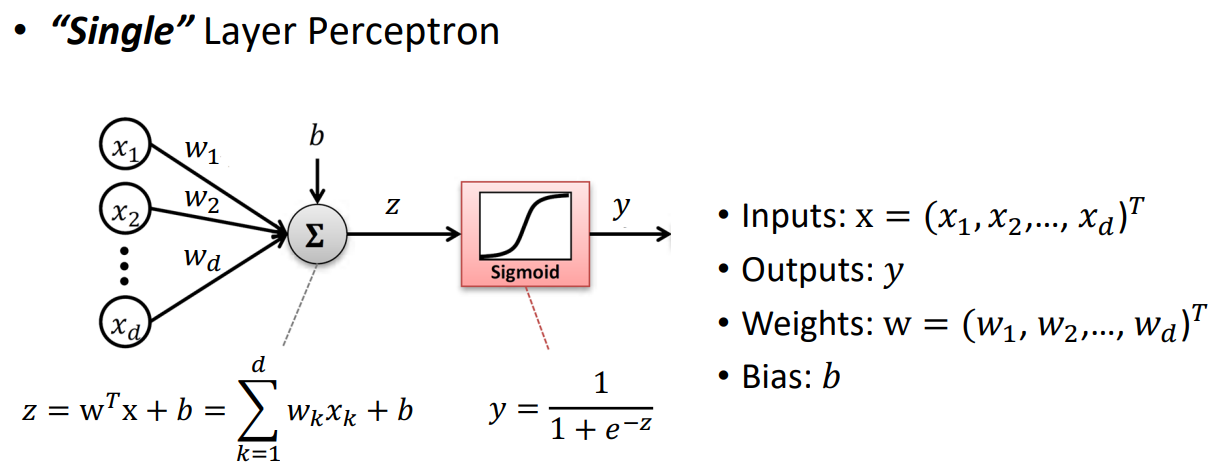
single layer perceptron 말 그대로 하나의 층의 퍼셉트론이다.
지난 공부에서 y = w0 + w1*x 라는 식에서 w0를 이제는 b라고 이해하면 된다.
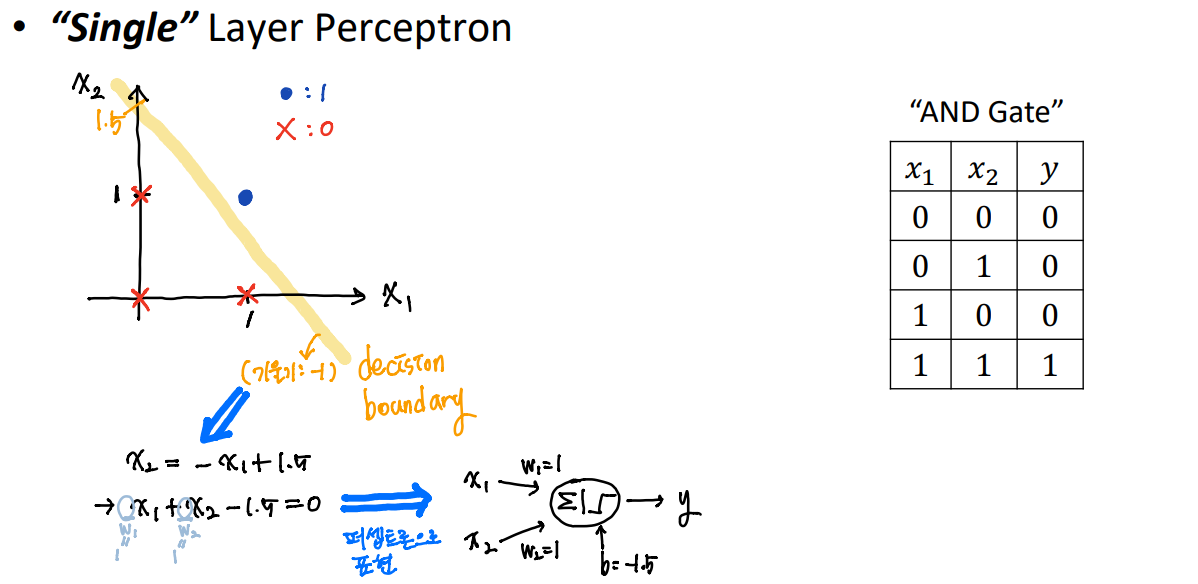
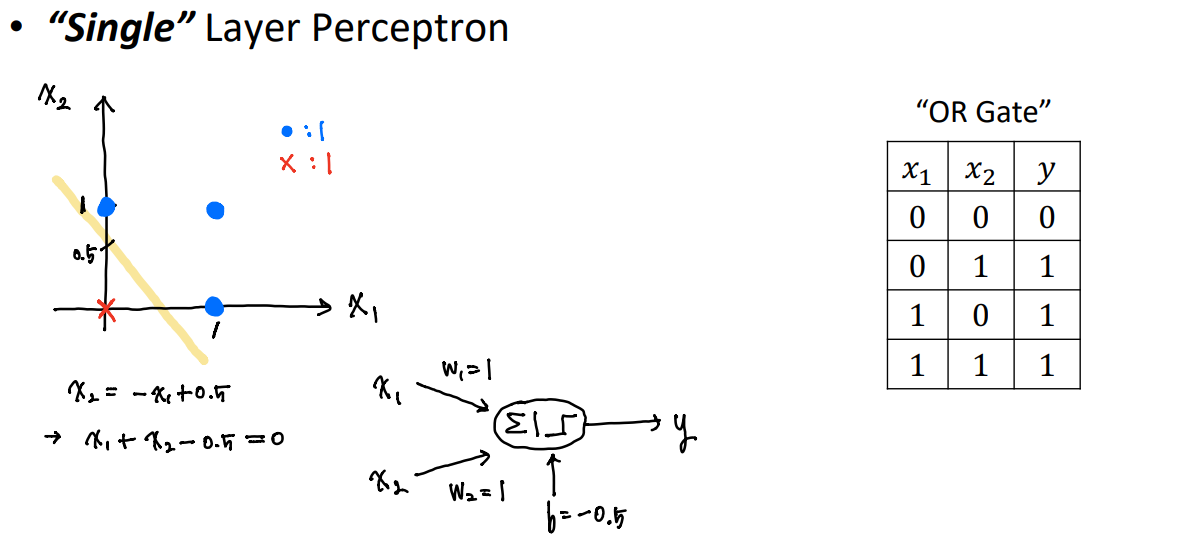

Single layer Perceptreon을 사용하여 XOR을 해결할 수 없다는 것을 주목해야한다. 그래서 나온 것이 Multi-layer Perceptron이다.
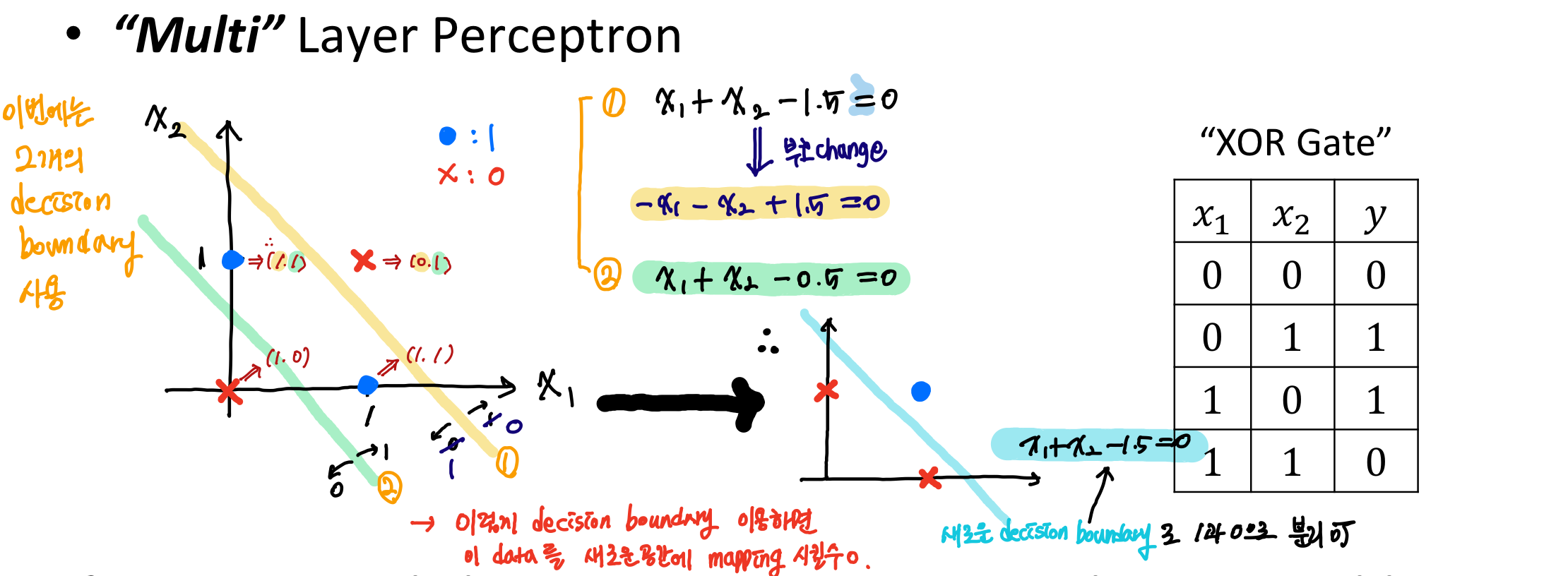
만약 우리가 2개의 Single layer Perceptreon(단일 레이어 퍼셉트론)을 사용한다면, 우리는 XOR 문제를 해결할 수 있다. 이 모델의 이름은 "Multi-layer Perceptron(다층 퍼셉트론)"이다.
2. Neural Network Presentation
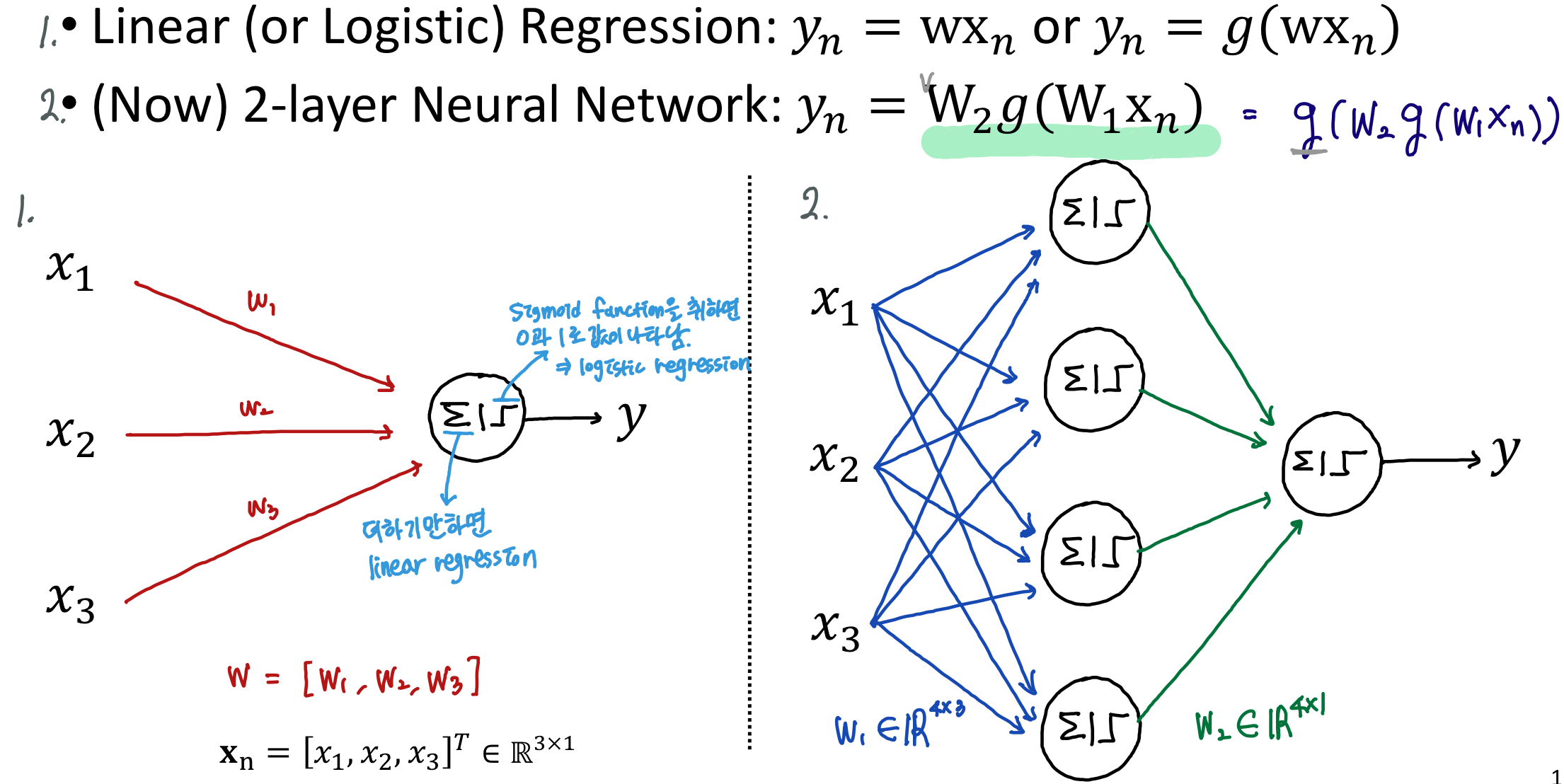
yn = w*xn <- continuous한 값을 구하면 linear regression이 된다.
linerar regression은 logistic과 달리 더하기만 하면 된다.
yn = g(w*xn) <- 0, 1 의 discrete한 값으로 나타내고 g함수는 시그모이드 함수이다. 따라서 logistic regression이 된다.
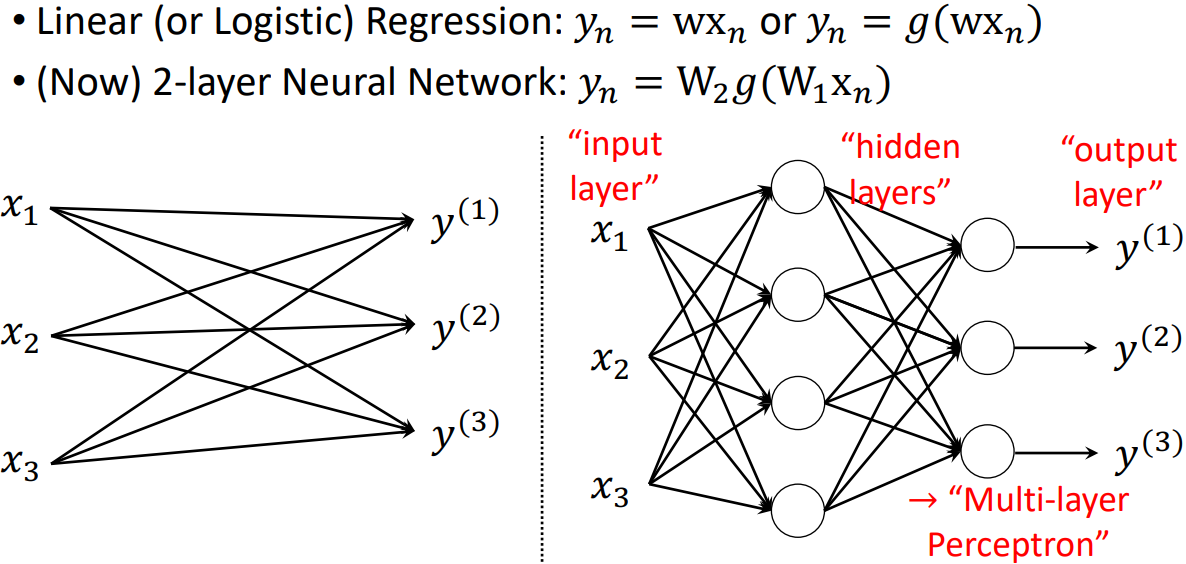
Multi-layer Perceptron은 위와 같이 히든 레이어를 가진 퍼셉트론이다.
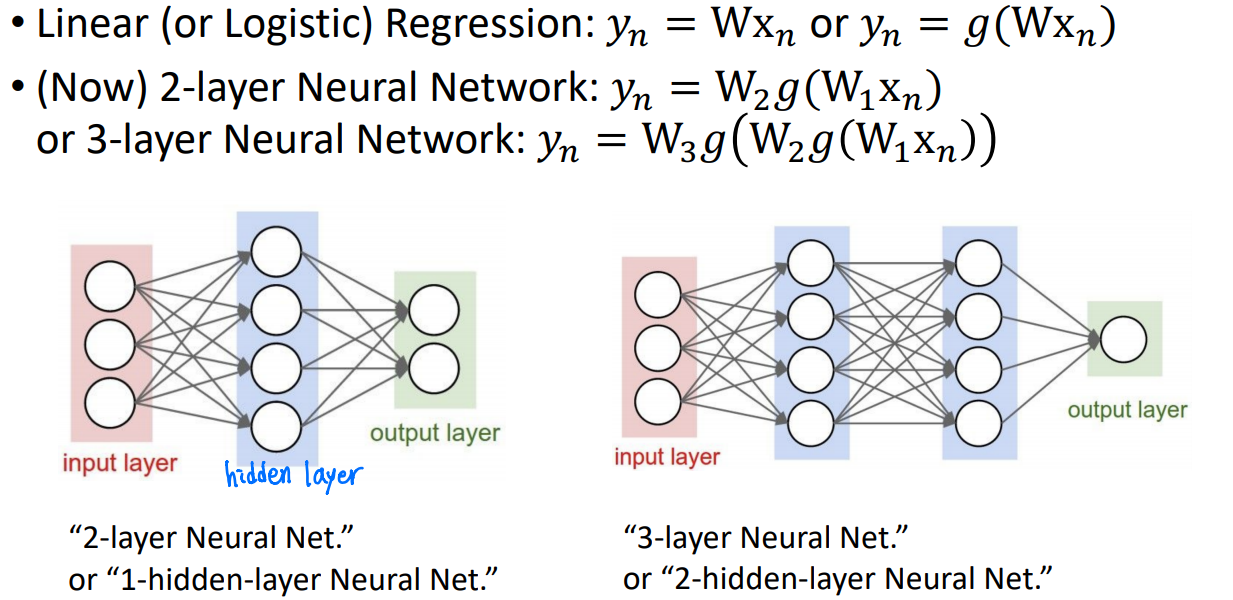
Perceptron은 매우 광범위한 용어이다. 이것들은 더 정확하게 "Fully-Connected Networks"라고 불린다. 네트워크가 모두 weight로 연결되어있기 때문이다. 또는 "Multi-Layer Perceptron (MLP)"이라고도 한다.
위 식에서 함수 g(z)는 Activation function(활성화 함수)이다. 활성화 함수는 시그모이드 외에도 다양하다. 활성화의 기능은 네트워크 기능에 non-linearity(비선형성)을 추가한다. linear하지 않는 데이터들이 많이 있는데, 거기에 non-linearity를 줌으로써 데이터를 더욱 잘 표현할 수 있다.
Q. 만약 activation function들이 없다면?
yn = w2*w1*xn, w3 = w2*w1 → wn = w3*xn => linear classifier가 된다.
마찬가지로 layer가 아무리 늘어나게되도 non-linearity를 주지 않는다면 linear classifier가 되기 때문에 표현할 수 있는 classification의 성능에 한계를 가지므로 우리는 적절한 activation function을 취해주면 된다.

ReLU는 대부분의 문제에 적합한 기본 옵션이다. 어느 정도 성능이 보장된다.
3. Computational Graph Representation

위는 파라미터를 업데이트하는 방법이다. cost들의 합을 Loss 함수로 정의하고 이 Loss 함수의 값을 최소화하는 w를 찾는 것이 목표이다. loss 함수 안의 파라미터 fw(xn)은 mapping function을 통한 아웃풋이고 yn은 실제 데이터의 아웃풋이다.
wj는 gradient descent 방법을 이용해서 파라미터를 업데이트하게된다.
But, gradient descent를 바로 사용하면 몇 가지 문제점들이 있다.
1) 매우 지루하고, 많은 계산량으로 기존의 컴퓨팅 파워로는 감당 불가능하다.
2) loss가 바뀌게되면 처음부터 모두 다시 계산해야한다.
3) 매우 복잡한 모델의 경우 실현 불가능하다.
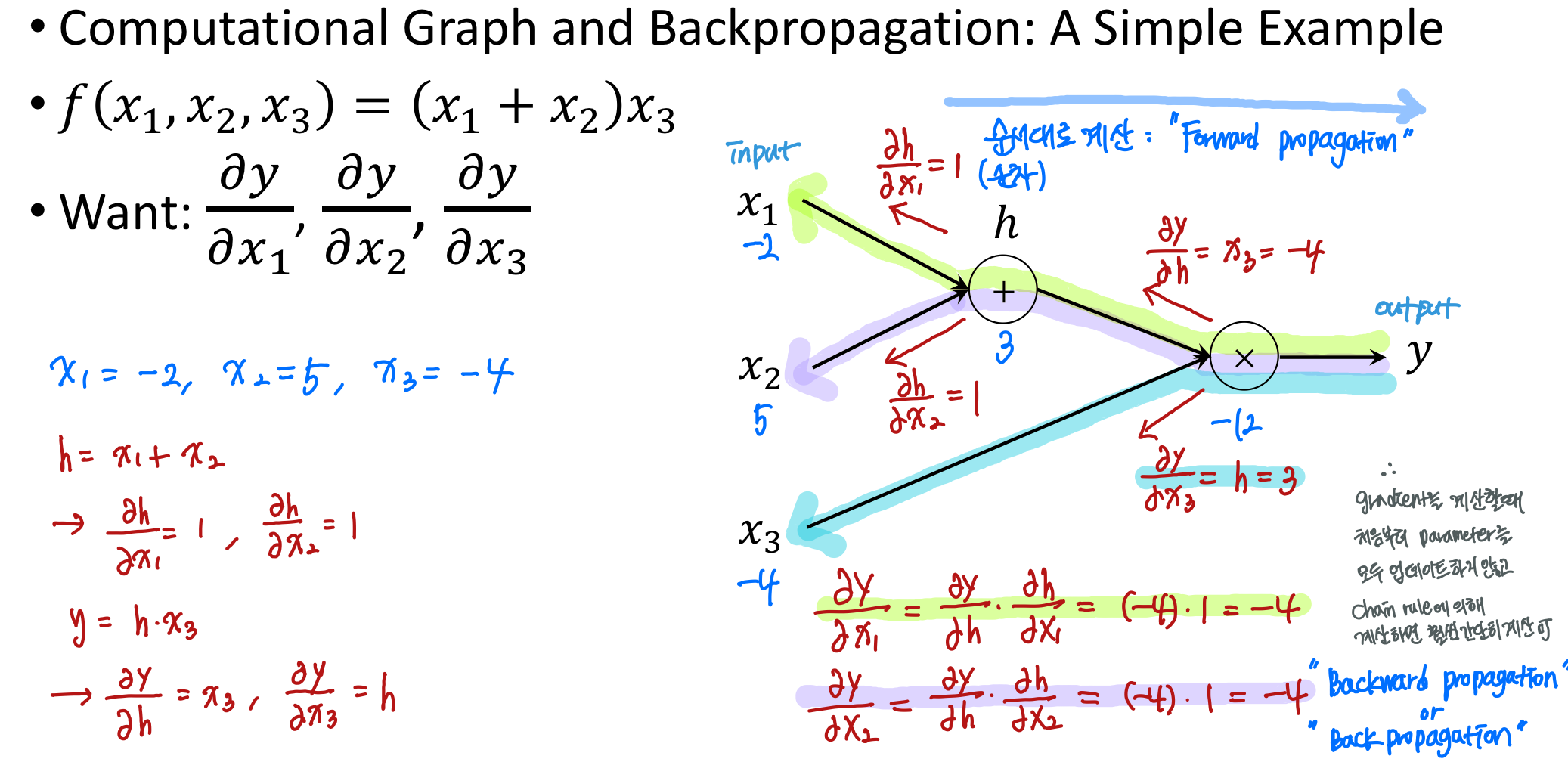
퍼셉트론을 위와 같이 conputational graph로 표현 가능하다.
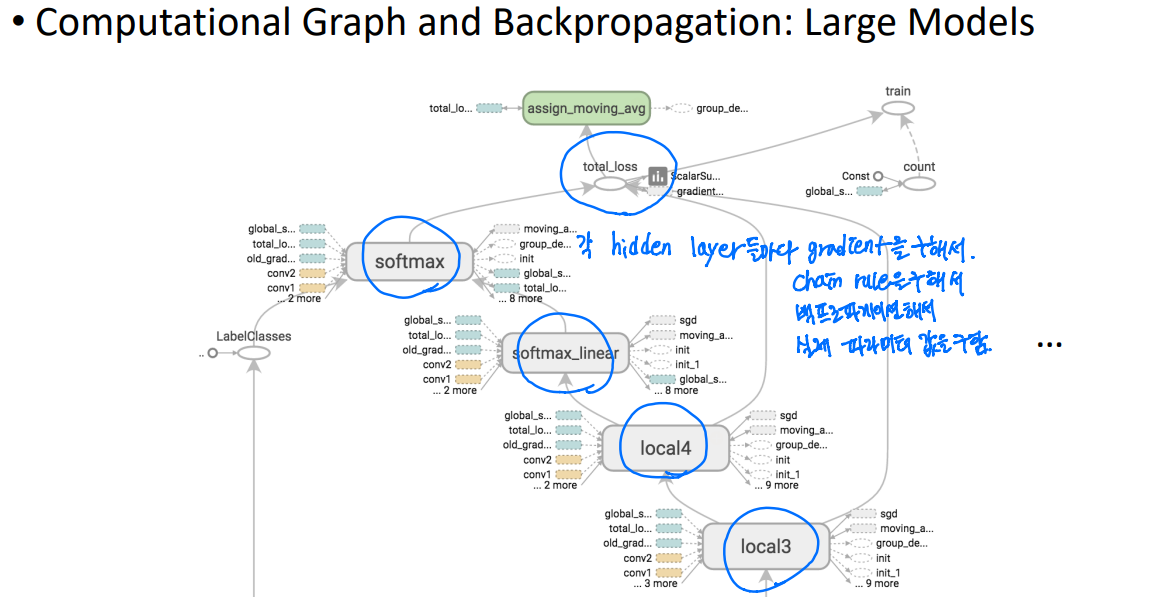
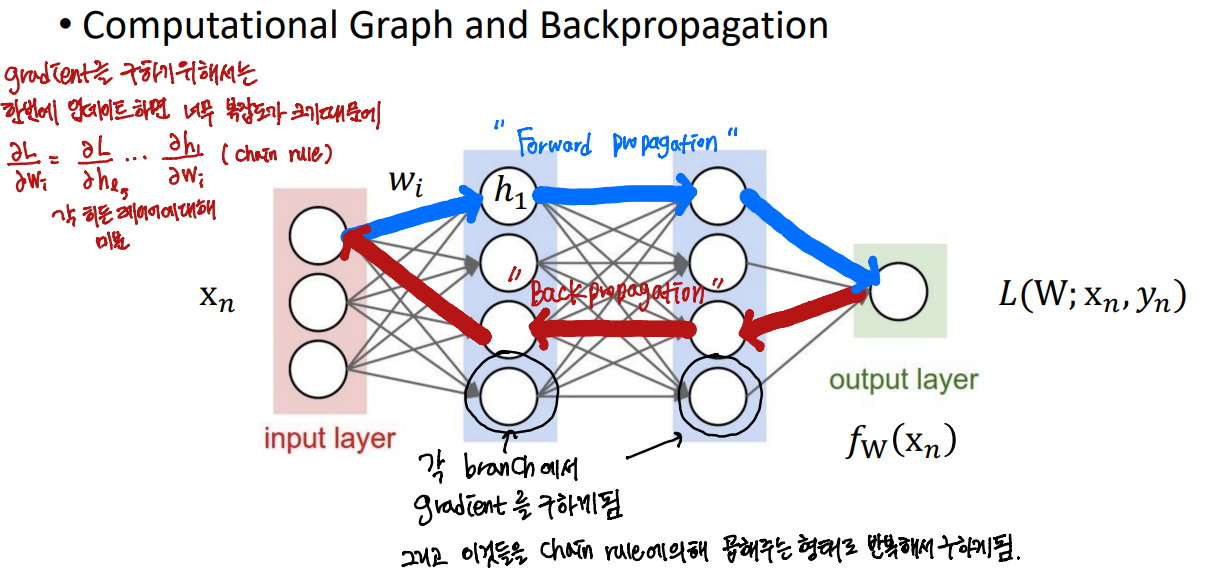
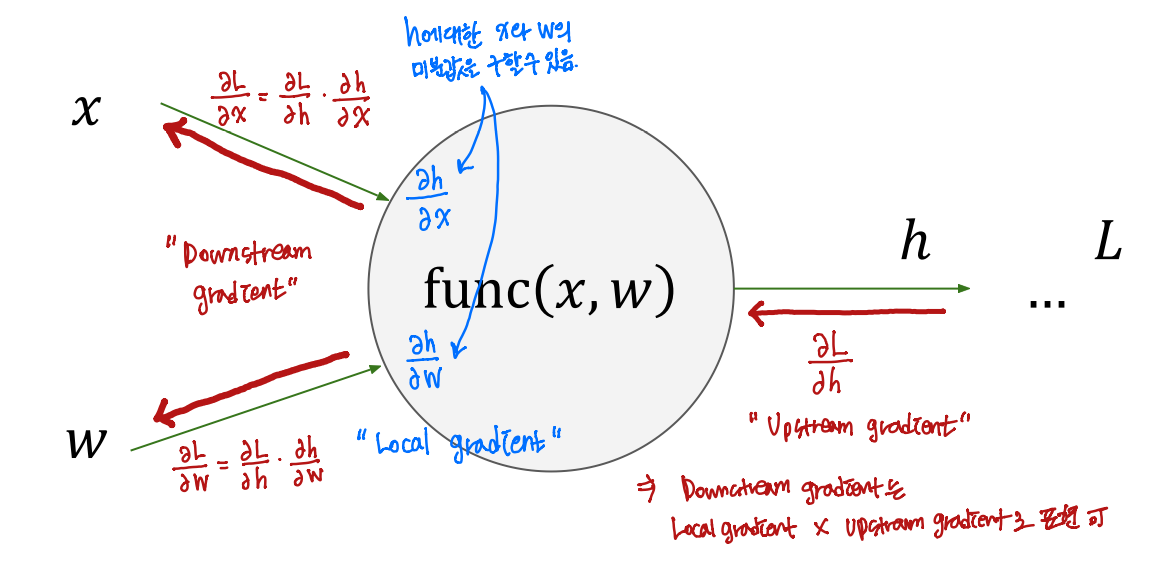
백프로파게이션을 하기 위해 기존의 gradient descent 방법처럼 모든 w에 대해 동시에 업데이트하지 않고 chain rule에 의하여 upstream gradient와 local descent를 곱해서 downstream gradient를 구하는 방식으로 derivative를 구한다.

x는 vector 형태이고 w는 matrix 형태이고, h는 vector 형태이다.
어떤 local gradient를 먼저 구해주게 될 때, 이것보다 forward 측면에서 살펴보면 다음에 수행되는 레이어인데, backpropagation을 하게 되면 미분이 계산되어서 들어오기 때문에 더 오른쪽에 있는게 upstream gradient가 되고, 그리고 upstream gradient x local gradient = downstream gradient를 구해주면 된다.
local gradient가 Jacobian으로 표현된다.
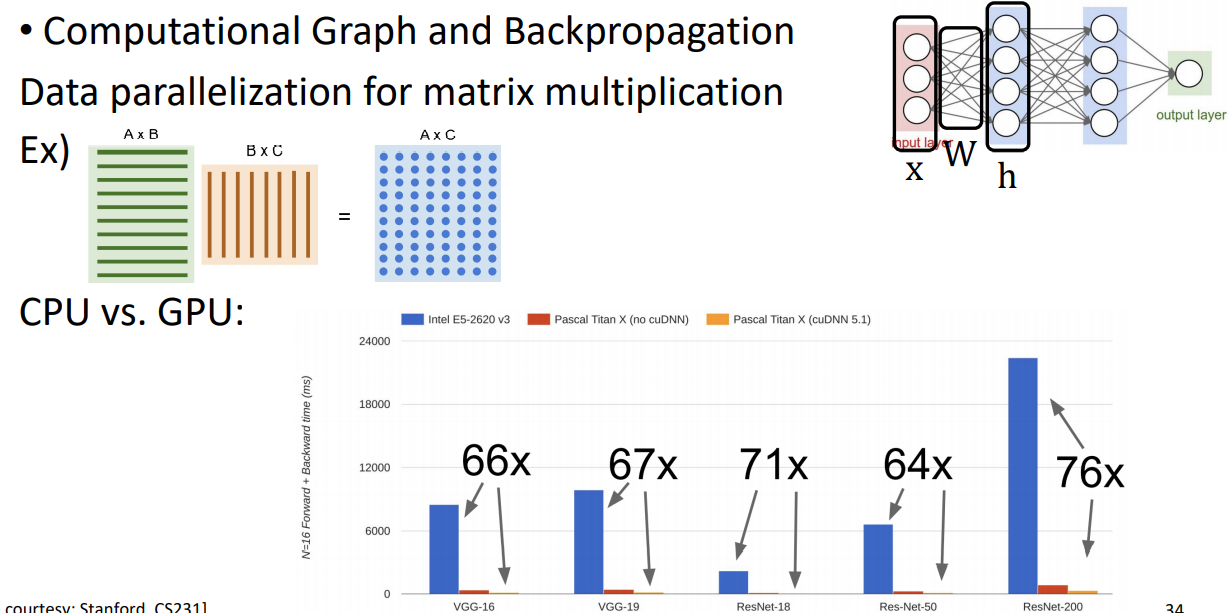
아래 그래프는 CPU와 GPU의 성능을 비교한 그래프이다. GPU사용할 때 66배 이상이 빨라지는 것을 알 수 있다. GPU 성능이 좋아지면서 matirix multiplication이 빨라지고 딥러닝 학습이 가능해졌다.
4. Derivative of Neural Network




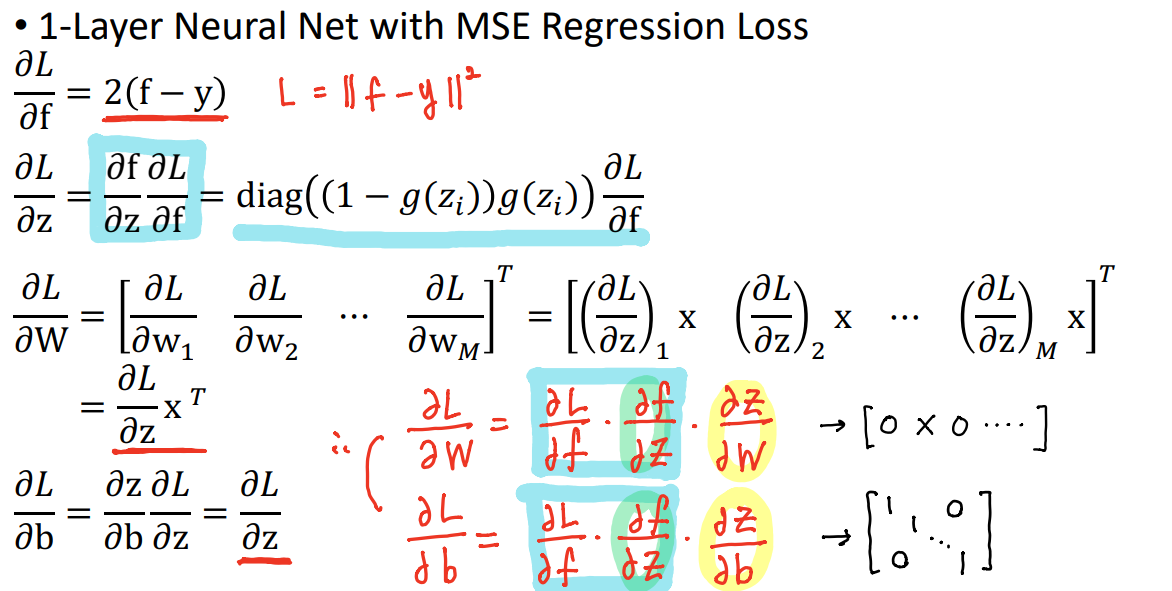
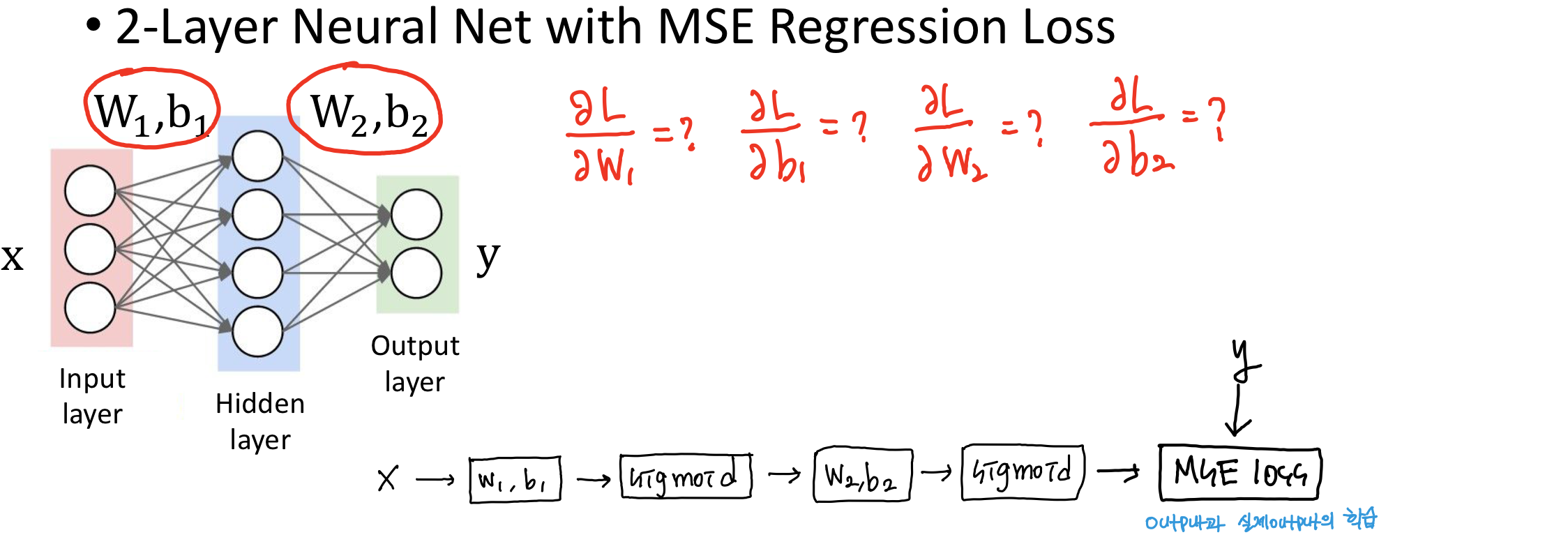
'전공 > 컴퓨터 비전' 카테고리의 다른 글
| [컴퓨터 비전] Introduction to Deep Learning (0) | 2021.04.20 |
|---|---|
| [컴퓨터 비전] Linear Regression and Logistic Regression (0) | 2021.04.14 |
| [컴퓨터 비전] Introduction to Image Processing (2) | 2021.04.07 |
