< TOPIC >
• 디지털 이미지 기본 사항
• 공간영역(Spatial Domain)의 영상향상
• 주파수 영역(Frequency Domain)의 이미지 향상
• Color Image Processing
1. 디지털 이미지 기본 사항
1) Image acquisition process
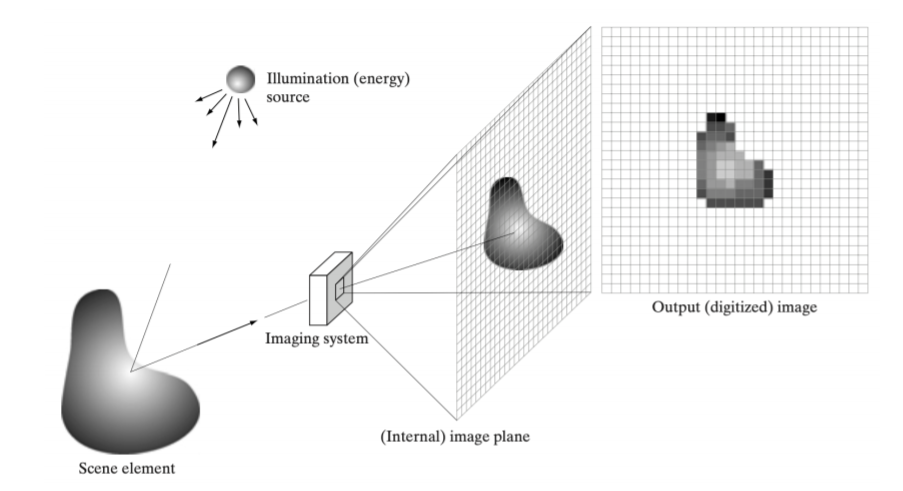
어떤 energy source로부터 어떠한 물체가 있을 때, 반사되어 빛이 들어온다.
이 때 Imaging system을 통해 영상이 투영되어 영상이 생성된다.
이렇게 아날로그 신호들이 system을 거쳐 디지털 정보로 저장된다. 그래서 최종적으로는 디지털 정보로 저장된다.
이 과정에서 원래 신호에서 sampling, quantization된 신호가 저장된다.
2)Image Sampling and Quantization
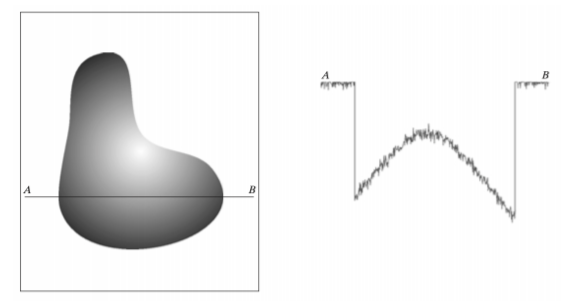
이러한 이미지를 스캔라인으로 그려보면, 값들이 노이즈도 섞여있고 영상의 intensity가 다음과 같이 변화하는 식으로 존재한다. 이 값들을 저장할 때는 모든 값을 저장할 수는 없기 때문에 아래와 같이공간측에서 sampling 과정을 거친다.
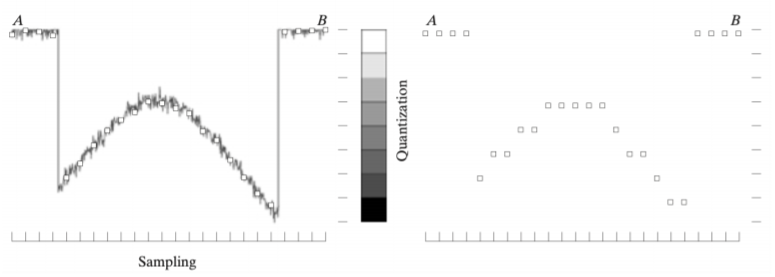
• sampling
→ 연속적으로 존재하는 신호들을 어떤 특정한 시간으로 쪼개어 sampling해서 거기에 해당하는 값들만 가져온다.
→ 공간측 영역에서 discrete하게 저장
• quantization
→ 값이 존재하는 범위가 continuous한데 이것을 디지털 신호로 저장할 때는 모두 갖고올 수 없기 때문에 일정한 범위로 쪼개어서 저장한다.
→ intensity 레벨에서 discrete하게 나누어 저장
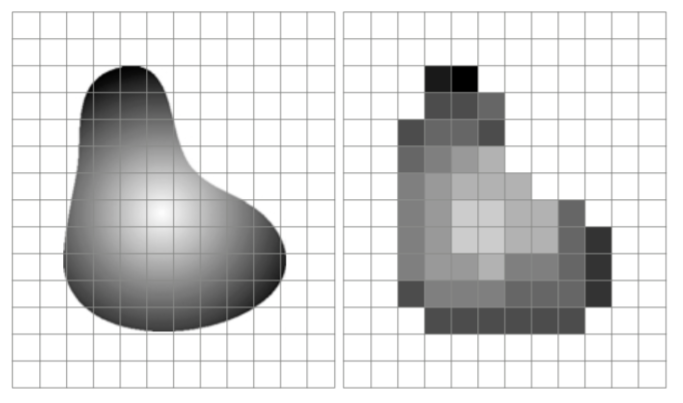
네모 단위로 나누어 sampling 되어 저장 &
흰색~검색까지 연속적으로 존재하였던 값들이 개수를 가지는 유한개의 값들로 나누어서 저장된다.
우리가 받아들이는 디지털 기계들을 이용해서 저장된 영상들은 항상 이렇게 샘플링 & quantization 과정을 거친다.
"화소가 높아질수록 화질이 좋아진다." 하는 것
→ 샘플링 간격이 좁아지고, quantization 간격이 점점 좁아지면서 가능해짐
3) Representing Digital Images
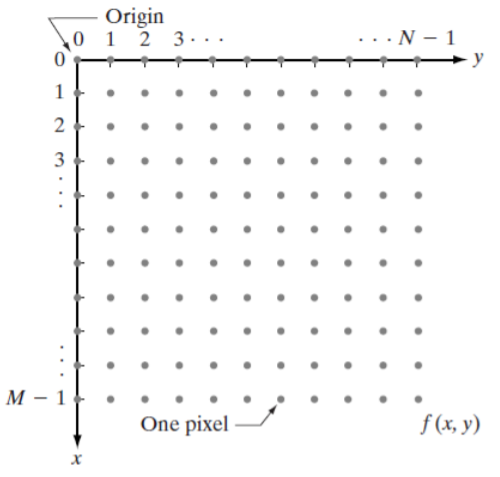
M x N digital Iamge는 공간적으로 샘플링되어있는 상태이다.
다음과 같이 좌표상에서 나타낼수있음
(0 <= x <= M-1, 0 <= y <= N-1)
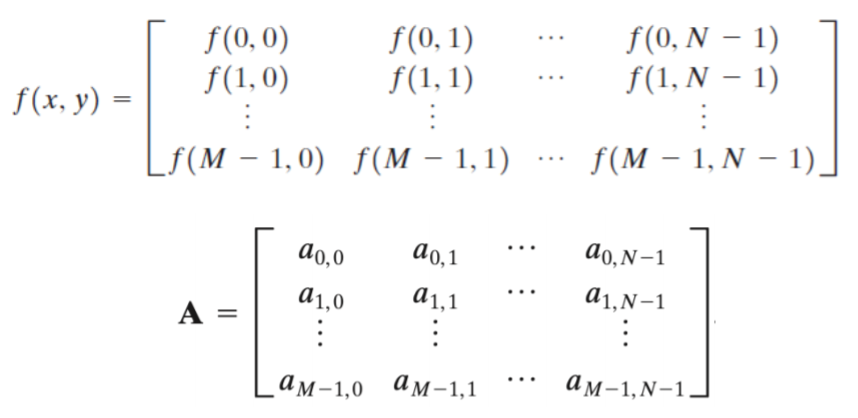
각 점에서 영상이 값을 가진다. 다음과 같이 함수로 표현할수 있다.
이렇게 함으로써 영상을 다룰 때 좌표로 표현하고 그 영상의 값들을 함수로 나타냄으로써 편하게 영상처리가 가능하다.
4) Shrinking / Zooming:
• Shrinking = subsampling = downsampling

1024x1024인 이미지를 512x512로 줄이면 → 4개의 픽셀에서 하나의 셀만 선택하게 된다.
→ 사이즈가 2배로 줄어든다.
• Zooming = oversampling = umsampling

- Nearest neighbor interpolation : using pixel replication
가장 가까운 픽셀을 선택해서 그 픽셀을 복사해서 사용하는 방법이다.
예를 들어, 1x1 픽셀을 복사해서 2x2 픽셀로(=4개) 만들면 -> 크기 2배 늘어난다.
그런데 하나의 픽셀을 복사하는 것이기때문에 화질이 좋지 않다.
32x32는 이 과정을 2번 거쳐서 128x128이 된다. 픽셀이 커보이게 된다.
단순히 픽셀값을 그대로 사용하는 것이기때문에 화질이 좋지 X
- Bilinear interpolation : using the four nearest neighbors of a point
원래 알고있는 1x1의 픽셀들로 빈칸을 채운다.
빈칸을 채우기 위해서 알고있는 서로 다른 값들을 이용해서 빈칸을 채운다.
픽셀들이 뭉쳐보이는 현상들이 좀 더 줄어들게 된다.
5) Basic Relationships between Pixels(픽셀에 대한 기본적인 관계들) --> 노트
• Neighbors of pixel
• Adjacency
• Distance measures
2. 공간영역(Spatial Domain)의 영상향상
1) Spatial domain operation
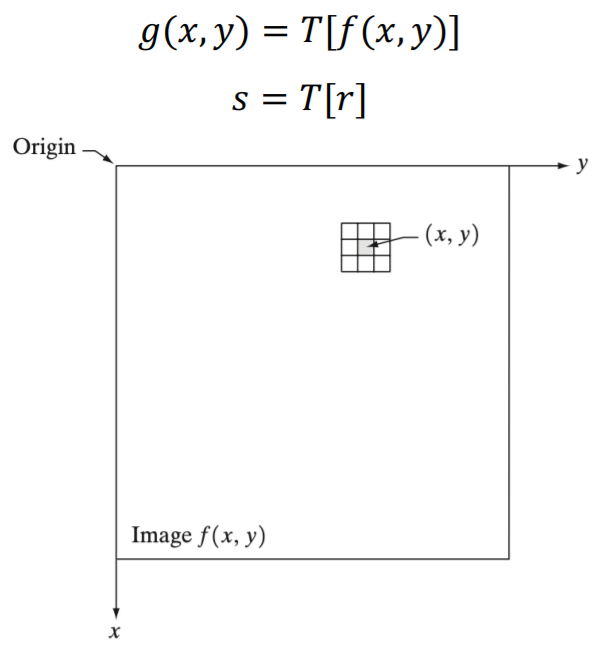
어떤 operation을 거쳐서 새로운 영상을 생성한다.
f(x, y)에서 어떤 transform을 거쳐서 새로운 영상 g(x, y)를 만든다.
Ex) Contrast stretching and Mask filtering
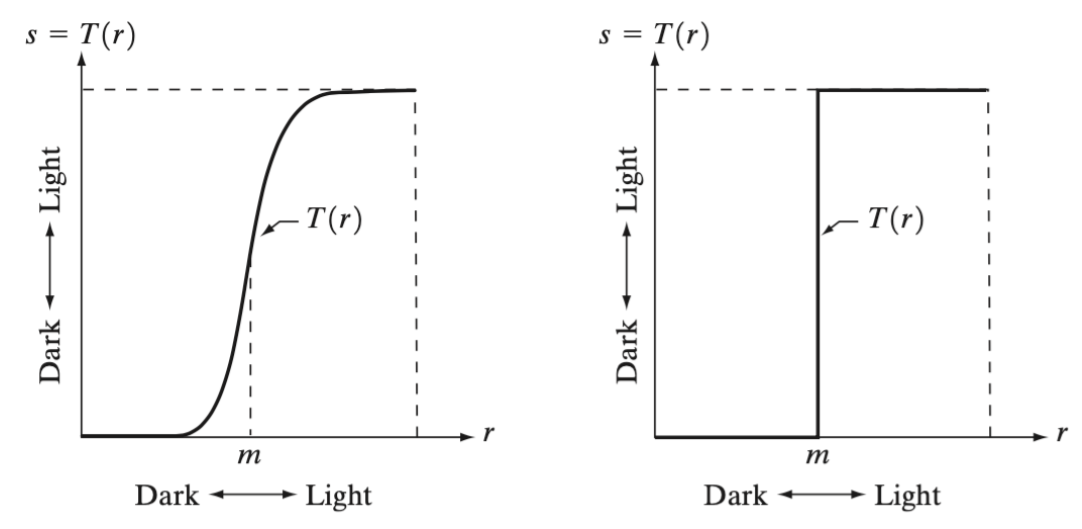
x축이 오리지널 영상이고 s는 transform을 거친 영상이다.
가장 어두운 black의 값은 0, 가장 밝은 white의 값은 256이다.
T라는 transform을 살펴보면, 영상이 m보다 작은 경우에 값을 0으로 tansform시키고,
m보다 큰 범위는 255로 transform시키는 것을 알 수 있다.
2) Basic intensity transformation

r이 오리지널 이미지, s가 transform을 거친 영상이다. s = T[r]
함수 y = x ⇒ s = r
⇒ 항상 같은 영상이 나온다.
⇒ Identity
negative transform은 y = -x + (L-1) ⇒ s = L - 1 - r
⇒ 영상이 반전된다.
이외에도 다양한 transform이 존재한다.
3) Basic grey level transformation
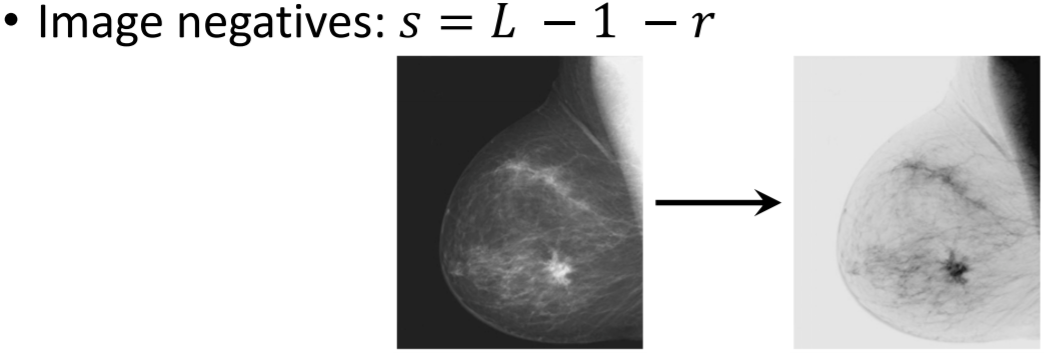
negative에서는 눈으로 보기에 더 분석하기 편하게끔 밝기를 반전시켜 변환가능하다.

log transform에서도 값은 작지만 분석요소들이 포함되어있을때, 눈으로 보면 보이지 않지만
이 트랜스폼을 거치면 어떠한 값들 존재하는 것을 발견 가능하다.
⇒ 시각적으로 더 잘 보이게하고 분석을 쉽게 한다.
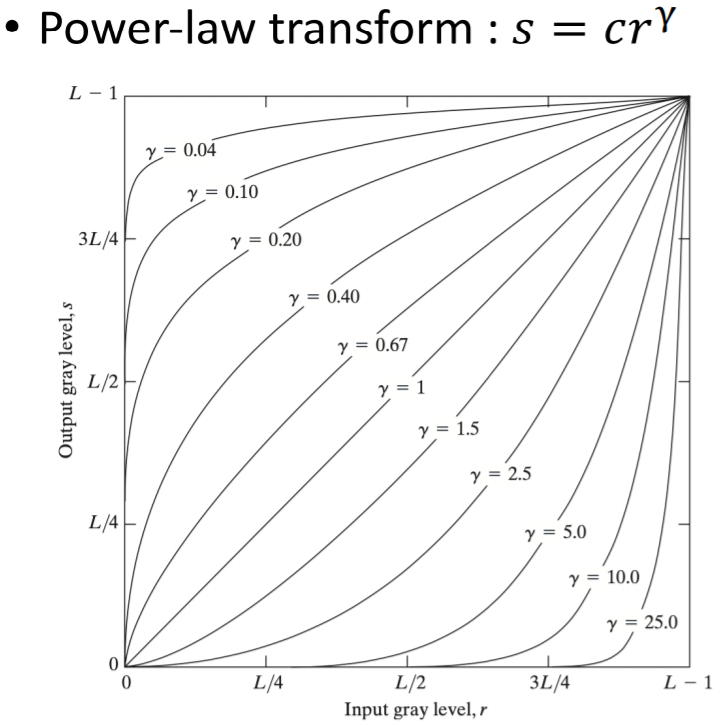
어떤 오리지널 영상에 대해
c와 γ를 적절히 사용해서 transform한다.
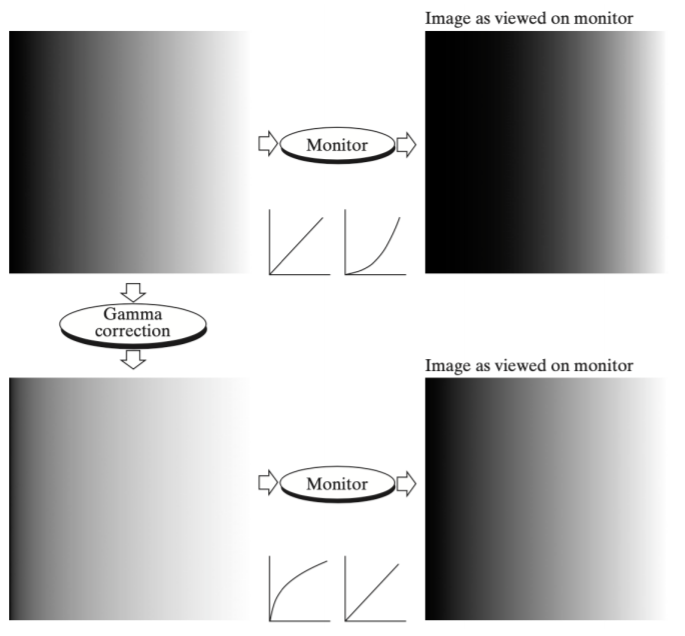
모니터 내부에서 하드웨어적 시스템을 거치면 transform이 일어나서 색깔이 좀 더 진해지고, 왜곡이 발생한다.
이것을 γ correction을 이용해 다시 모니터상에서 한다면 실제와 비슷한 색을 가진 영상을 보기 가능하다.

이외에도 위성에서 찍은 사진이 원본에서는 잘 보이지 않지만, 위와 같이 transformation 과정을 적절히 하면 발전한다.
4) Contrast stretching
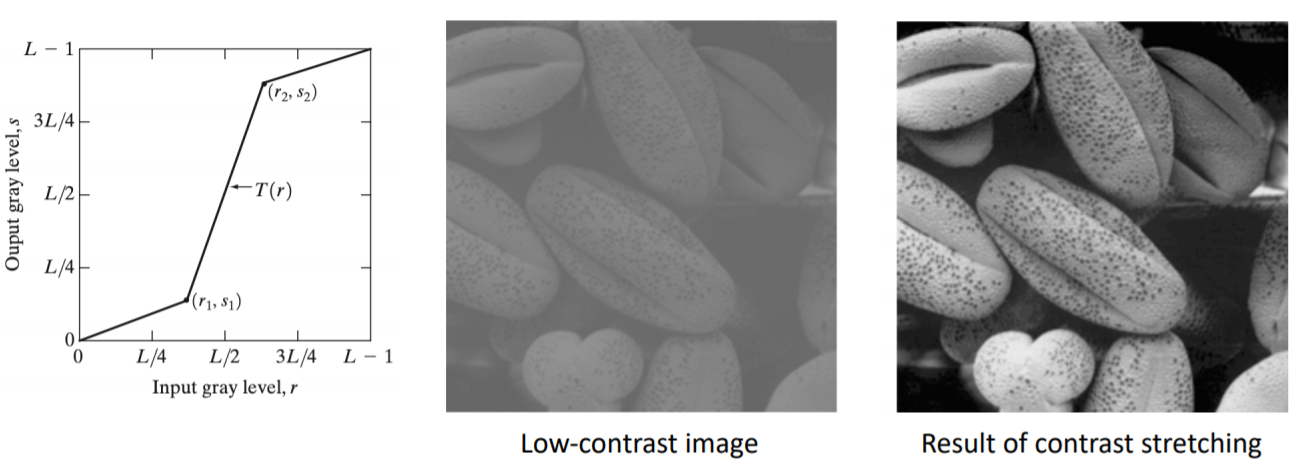
x축의 0 = 어두움, 맨 오른쪽 = 밝음 = 255
low contranst image → 어두움~밝음 영역 사이에 고루 영상이 분포하면 선명한 영상이 가능한데,
contrast가 작으면 일정한 부분에 많이 존재해서 영상이 흐려보인다.
그래서 이것을 전체 영역에 constrast stretching을 하여 전체영역에서 선명하게 보이게하려고한다.
5) Gray-level slicing

x축의 A~B 사이의 값 intensity에 해당하는 영상만 다음과 같은 값을 가지도록 하고, 나머지는 dark한 값을 가지게 한다.
기본적으로는 identity를 따라가는데, A~B 사이에만 특정한 값으로 밝게 적용된다.
⇒ 특정역역의 부분만 보고싶을때 이용한다.
6) Image filtering

noise를 줄인다던지, 영상을 밝게한다던지 등의 용도로 filtering을 사용한다.
이런 필터링을 어떻게 수행될까? ⇒ spatial 영역 / frequency 영역
7) Basics of Spatial Filtering
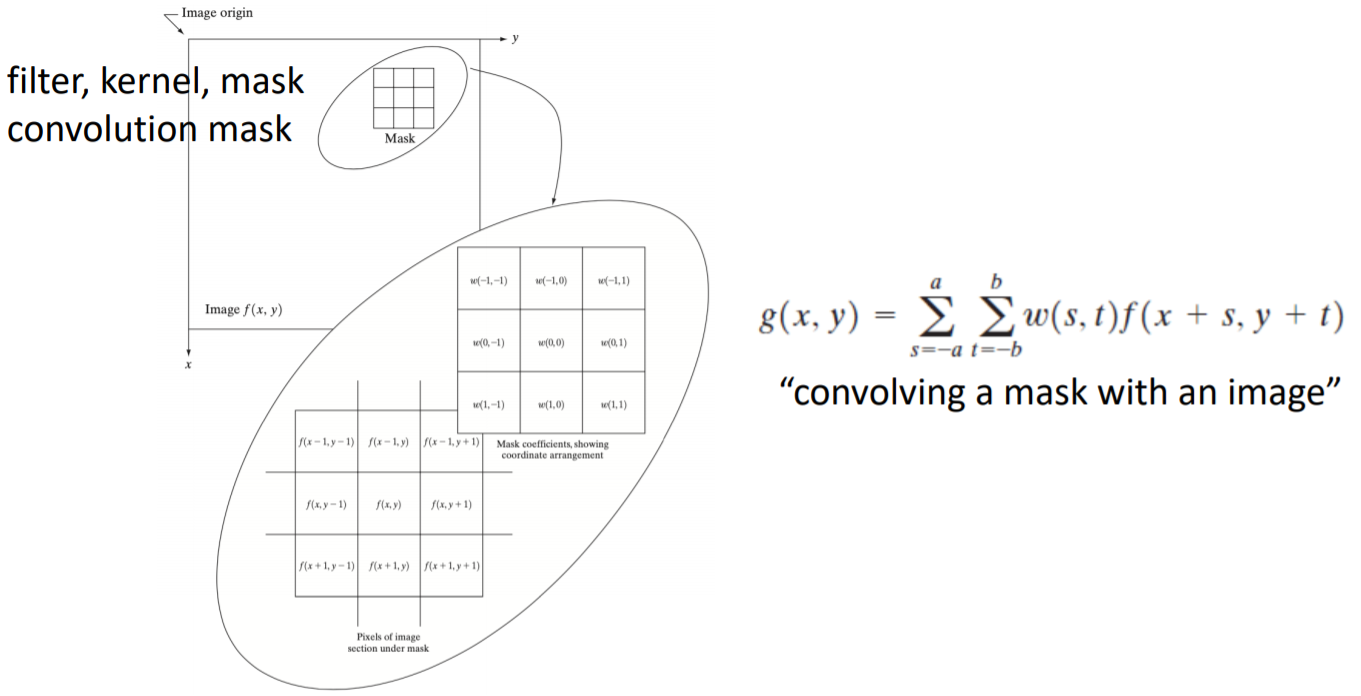
다음과 같이 영상이 존재하면, 이 영상에는 영상을 구성하는 f(x, y)로 표현된다.
이 영상에 적절한 mask를 씌워서 영상과 mask를 convolution을 함으로써 filtering을 수행한다.
mask = filter = kernel = convolution mask ← 다양한 용어
//영상과 마스크를 g(x, y)를 통해 ~ 필터링
8) Smoothing spatial filters
① Smoothing linear filters (averaging filters)

(smoothing = 흐리게하는 방법)
smoothing linear filters(= averaging filters)은 가장 간단하게 생각할 수 있는 방법이다.
어떤 값들을 주변에 이웃하는 값들과 averaging을 시키기때문에 값이 흐려진다.
중심부에 좀 더 가중치를 주고 싶다면, 가운데를 4, 동서남북을 2 이런식으로 가중치를 주고, 항상 합이 1이 되도록 normalization을 해줘야한다. 여기에서 1/16을 곱하지 않으면 전체 픽셀의 값이 커지기때문에 영상이 과도하게 밝아진다. 꼭! 항상 계수들의 합으로 normalization을 해줘야한다.
② Order-statistics filters
ordering을 이용한 필터, 즉 non-linear spatial filters이다.

sorting을 시켜보면, 가장 작은 값이 10, 가장 큰 값이 100이다.
- min filter : 가장 작은 값을 취한다.
- median filter : 중간 값을 취한다.
- max filter : 가장 큰 값을 취한다.
이 중에서 median을 가장 많이 사용한다.
ㅡ→ impullse noises (salt-and-pepper noise) 를 제거하는데 효과적이다.
(ex. 영상의 값들이 주로 5인데 impulse noises가 들어가면 갑자기 0, 30 이런식으로 들어간다. 그런데 이것을 median 값들을 취하게 되면, 가운데 값이 선택되니까 5가 선택돼서 noises를 쉽게 제거 가능하다.)

3x3 averaging 필터를 사용하면 노이즈가 잘 제거가 안되지만, 3x3 median 필터를 사용하니까 노이즈가 잘 제거된다.
③ Gaussian filter
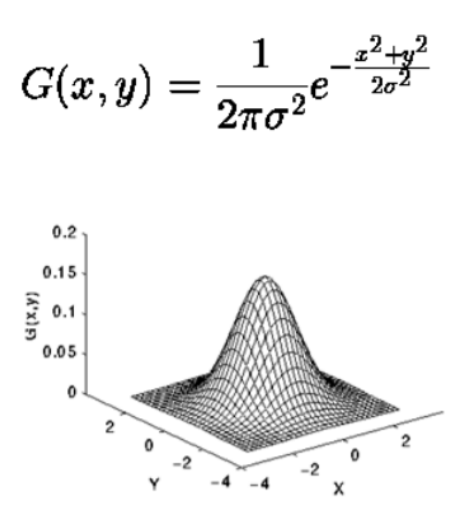
통계학적으로 샘플링하는 수가 많을때 가우시안 분포를 따라가는 것을 가정한다.
가우시안 필터를 사용해서 노이즈를 제거한다.
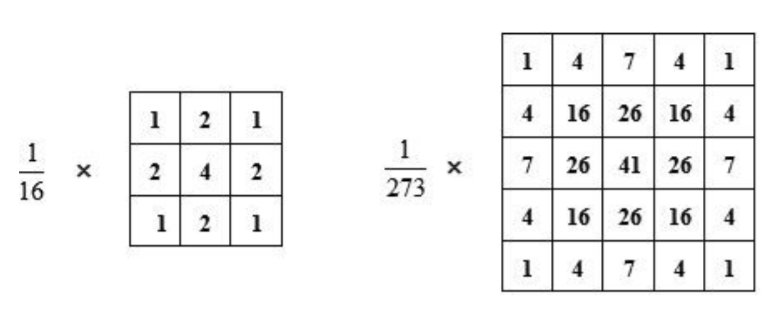
연속적인 값들을 3x3이나 5x5로 표현하면 다음과 같다.
average filter의 일종이다. 가중치가 조금 들어간다.
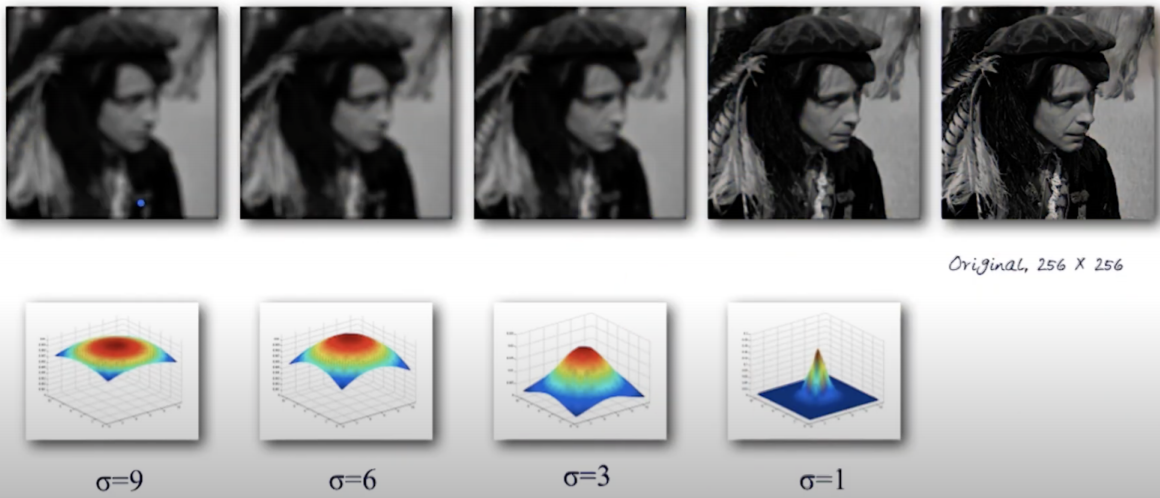
가우시안 필터를 취했을 때의 결과이다.
σ = 1일때는 스무딩이 덜 되고 가운데 값이 중점이다.
σ 가 커질수록 스무딩이 커지면서 영상이 흐려진다.
9) Sharpening spatial filters
→ 영상을 더 선명하게 보는 방법
1차원 함수 f(x) 의 정의
• first-order derivative
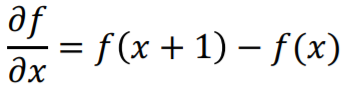
• second-order derivative
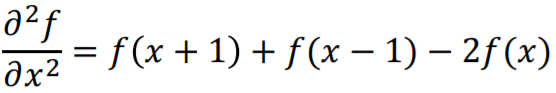
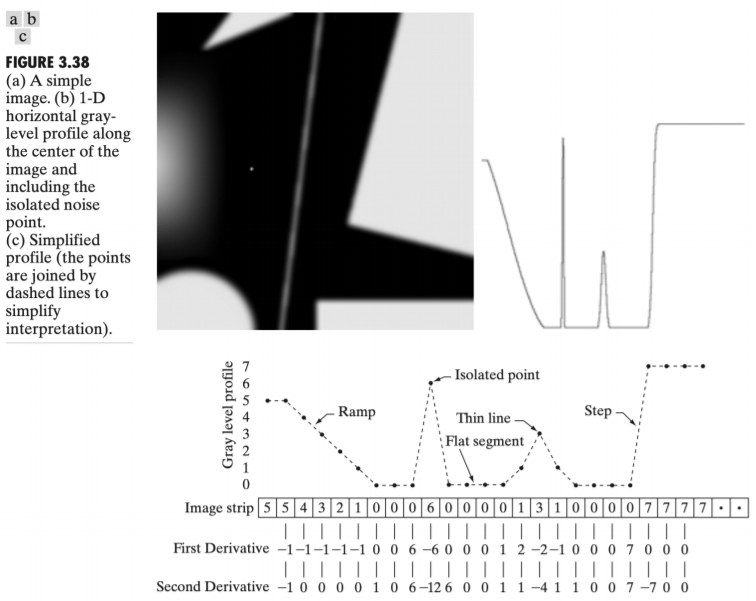
/*어두워지면 intensity 줄어들고, 밝은 부분에 값이 올라간다. //보충
이 값들의 실제 intensity를 숫자로 표현~
fist derivative = f(x+1) - f(x)
second <- 또 뺌
흰-> 검 부분. 값이 줄어드는 부분에는
-> fisrt는 음수
-> second는 일정속도로 줄어드니까 값이 0
어떤 point가 생기면
값이 증가
second는 가운데 값이 음수*/
① The Laplacian
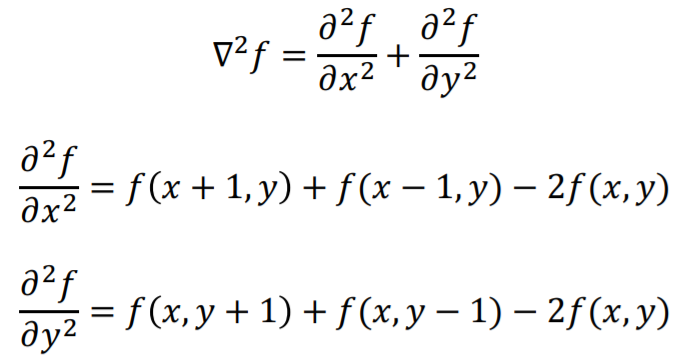
Laplacian은 2차원에서 정의된다.
x축, y축에서 각각 second-order derivative를 더해서 기호로 표시한다. //뭔말
digital form은 아래와 같다. 위 x, y에 관한 식을 더해서 표현한다.

필터 마스크로 나타내보면 첫번째 3x3 정사각형 //아이패드 보충
Laplacian을 취하게 되면 영상에서 급격한 변화가 일어나는 곳에 값이 생기기 때문에 edge 영역에서 값이 크게 나오는 것을 확인할 수 있다.
image enhancement을 위한 2차원, second-order derivatives은 다음과 같다.
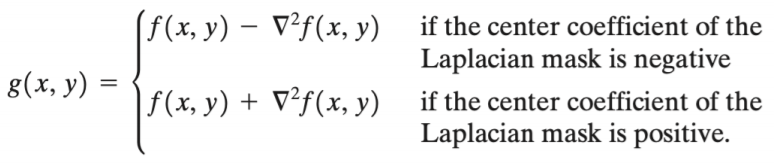
기본 영역에서 에지 영역을 빼거나, 더함으로써 영상을 필터링한다.
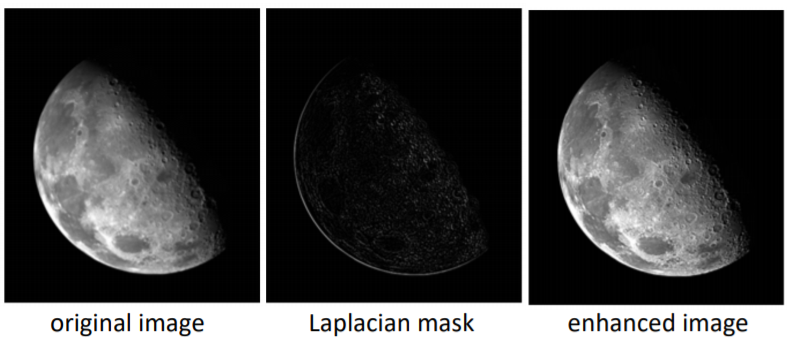
두 식 중, 아래 식을 적용해보면,
original image(1번째 사진) → f(x, y)
Laplacian mask(2번째 사진) → ∇^2f(x, y) ←ㅡ 에지나 텍스쳐가 많은 영역에서만 값이 크게 나타난다.
enhanced image(3번째 사진) → 이 두 식을 더하면 에지 영역이 더욱더 강조되기 때문에, 조금 더 선명한 영상으로 필터링된다.
//아래 식 보충
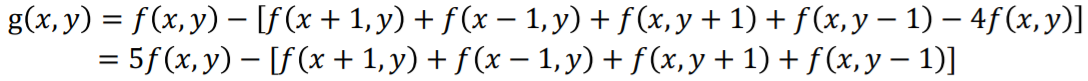

원본 영상에서 Laplacian mask가 negative일 때는 빼서 sharpening 가능하다.
원본 영상에서 ∇^2f(x, y)가 에지나 텍스쳐 정보를 갖고 있기 때문에,
폰네이버?를 이용한 Laplacian mask를 사용하면 2번째 그림처럼 나타나고,
8네이버?를 이용하면 3번째 그림처럼 더 선명하게 나타난다.
② The Gradient

Gradient는 값이 변화하는 부분에서 생긴다.
→ edge나 texture 정보를 가지고 있는것을 확인할 수 있다.
Gradient 자체는 방향성을 가진다.
Gradient 크기를 구하면 방향성말고 값만 나온다.
magnitude = 각 컴포넌트 제곱의 스퀘어 루트
이것을 이용해서 그래디언트를 구한다.
조금 더 간단히 필요하면, 각 절대값을 더하는 것도 크기가 많이 차이 나지 x
이런 gradient 를 이용한 operator가 sobel operator이다.

어떤 영상에서 다음과 같이 에지나 텍스쳐가 변화가 있는 영역을 필터링을 거쳐 표현 가능하다.
이 그림에서는 원 둘레에서 에지가 생기기 때문에 여기서만 값이 크게 나타난다.
10) Combining spatial enhancement methods
여러 필터링 기법을 사용해서 영상을 어떻게 향상시킬 수 있는지 알아보겠다.
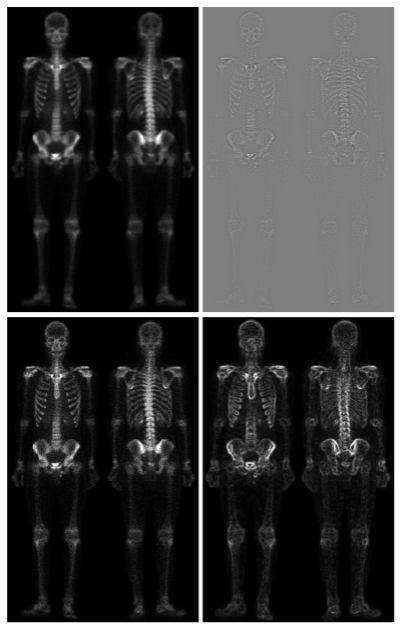
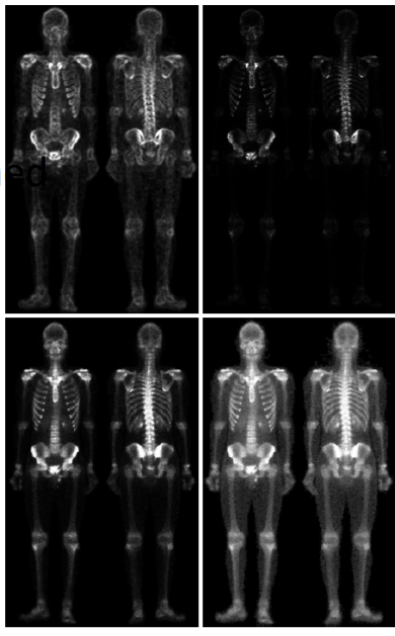
1. Original image
2. Laplacian mask 사용
→ 에지 영역만 보이게 된다.
3. 1번 그림(오리지널 이미지) + 2번 그림(라플라시안 마스크 적용)
→ 더 선명해짐
4. sobel operator 적용
5. sobel operator 취한 이미지에서 5x5 averaging filter를 이용해서 스무딩 시킨다.
6. 그렇게 스무딩된 영역에서 어떤 특정한 값 이상만 남겨두고
나머지는 어둡게한다.
→ 그럼 그 부분만 강조됨. 보고자하는 값들이 더 밝아짐
7. original image + 2.에 의해 얻어진 샤프닝된 이미지
8. 여기에 power-law transformation을 거쳐서 나온 최종적인 영상
이런식으로 다양한 기법을 통해 형성된다. 영상에서 어떤 부분을 보고싶은지, 어떤 스무딩, 샤프닝 등이 필요한지 모든 도메인마다 다양한 필터링이 필요로 한다. 그런 필요로 하는 필터링이나 트랜스포메이션에 맞춰서 영상을 변형시켜 사용할 수 있다.
3. 주파수 영역(Frequency Domain)의 이미지 향상
1) Fourier Transform and the Frequency Domain
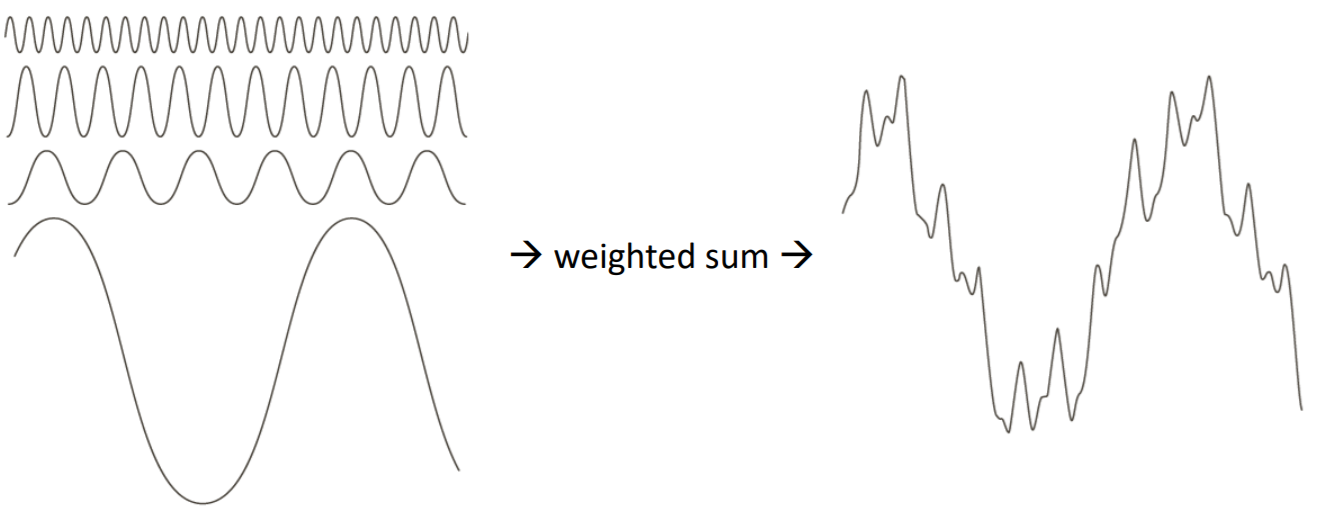
Fourier transform : 어떤 신호를 sin과 cos으로 이루어진 다양한 주기함수로, weighed sum으로 표현할 수 있는 것
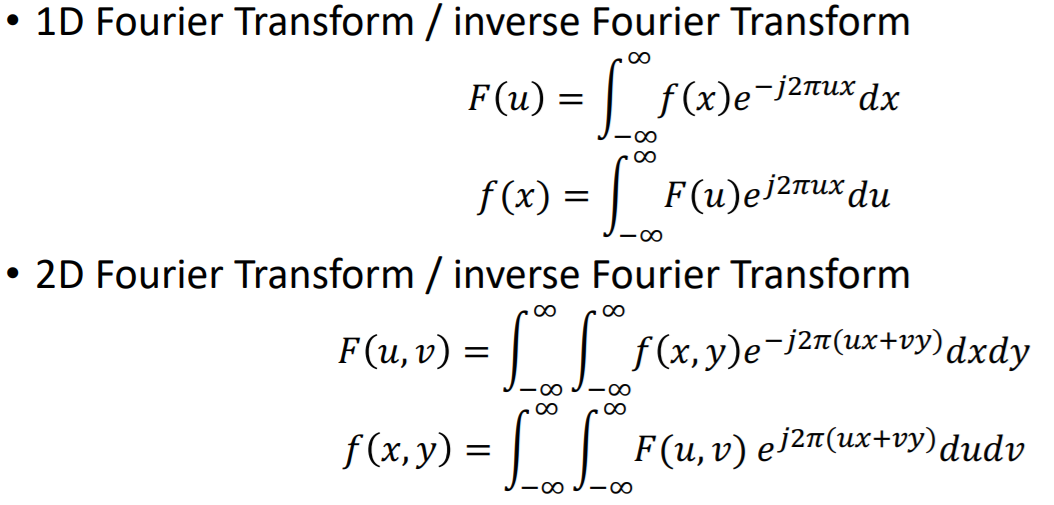
어떤 신호가 존재할 때 이것을 Fourier transform을 하면, 각 주파수 도메인에서 어떤 주파수를 갖는 신호들의 coefficient?가 어떻게 되는지 Fourier transform을 통해 구할 수 있게 된다.

그런데 우리는 discrete한 신호를 다룬다. 1D discrete Fourier transform은 continuous한 신호이기 때문에 적분을 했지만
여기에서는 sum을 이용해서 discrete Fourier transform을 수행 가능하다.
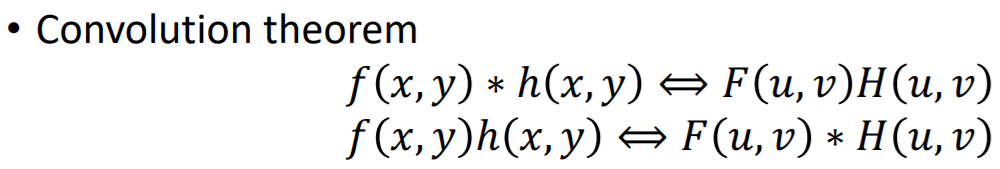
알아둬야할 것은 Convolution theorem !
spatial domain에서의 convolution은 → frequency domain에서는 곱이 되고,
spatial domain에서의 곱은 → frequency domain에서는 컨볼루션이 됨
만약에 filter size가 같으면, spatial domain서는 convolution을 모든 픽셀마다 수행한다.
근데 이걸 frequency domain에서 하면 곱으로 간단히 가능하다.
2) Filtering in the frequency domain
Frequency domain에서 영상을 필터링하는 과정은 다음과 같다.
0. 먼저 영상 f(x, y)를 discrete Fourier transform(DFT)을 거쳐서
1. 푸리에계수 F(u, v)를 구하고
2. 여기에서 spatial domain convolution을 수행했는데, 그게 Convolution theorem에 의해서 F(u, v)*H(u, v)
3. 다시 inverse discrete Fourier thransfor(IDFT)를 취해서
4. 필터링된 영상 g(x, y) 획득 가능
spatial domain에서는 필터를 average filter라던지, Gaussian filter 라던지 등등.. 했는데,
frequency domain에서는 필터링을 어떻게 설계해야 스무딩, 샤딩이 되는지 살펴볼 것!
3) Lowpass filter
어떤 영상에서 텍스쳐가 많거나 에지가 있는 영역들은 frequency가 일반적으로 높다.
반대로 homogeneous한 영역은 프리컨시가 낮음
에지나 노이즈들을 제거하기 위해서는 high frequency를 사용하지 않고, low frequency만 pass하면 영상이 전체적으로 스무딩되고 블러되는 특성이 있다. 그래서 이렇게 frequency가 낮은 부분들만 통과하는 것을 Lowpass filter라고 한다.
① ideal lowpass filter
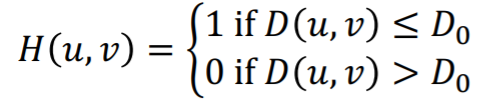
ideal lowpass filter같은 경우는, 어떤 반지름이 D0인 영역 이내의 frequency만 통과시키고 나머지는 0으로 보내버린다.
이 필터는 다음과 같이 어떤 D0보다 작은 부분만 살리고 나머지는 모두 0으로 보낸다.
spatial domain에서는 Fourier Transform을 하면서 신호가 +, -가 반복하면서 ringing effect가 생긴다.
ideal lowpass filter를 통해 다음과 같이 필터를 수행하면, 필터의 크기가 작으면 괜찮지만
크기가 크면 위와 같이 ringing effect가 생겨서 영상이 왜곡된다. //a 그림 아이패드 보충
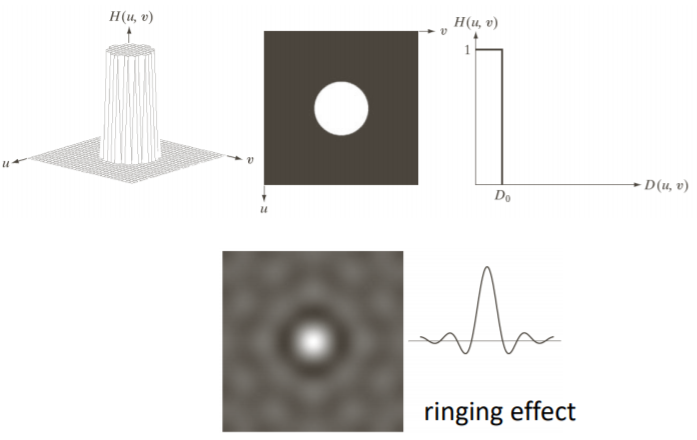
② Butterworth lowpass filter
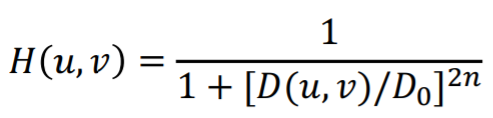
이걸 극복하고자 butterworth lowpass filter가 개발됐다.
ideal lowpass filter처럼 딱 떨어지게 하지 않고 smooth하게 떨어지게 설계했다.
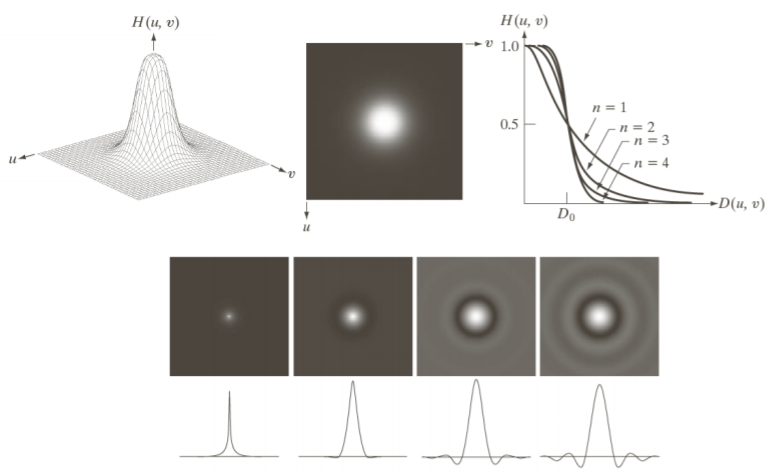
하지만 n의 값이 작을 때는 잘 통과하는데, n이 커지면서 ringing effect가 생긴다.
③ Gaussian lowpass filter
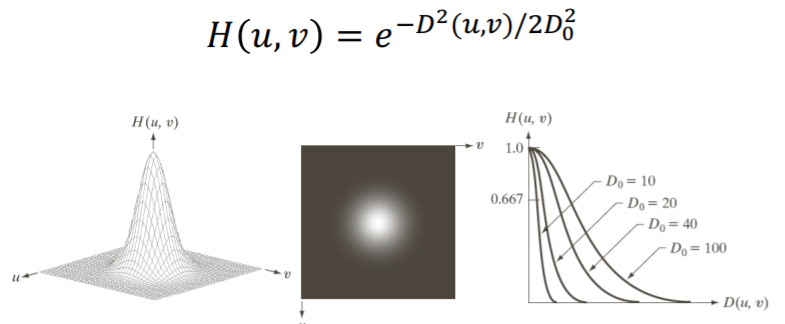
그래서 많이 사용하는것이 Gaussian lowpass filter이다.
spatial domain에서도 Gaussian lowpass filter을 따르고,
frequency domain에서도 Fourier Transform을 따랐을 때 Gaussian lowpass filter을 따른다.
ringing effect가 스패셜 도메인에서 발생하지 않기 때문에, 영상이 스무딩된다. (오른쪽 4번째 그림) //아이패드 보충
frequency domain에서 어떤 영상을 가운데 부분만 통과시키고 나머지 부분은 제거된다.
high frequency 영역의 존재할 수 있는 텍스쳐라던지 에지 정보가 사라져서 스무딩되는 효과를 가진다.
4) Highpass filter
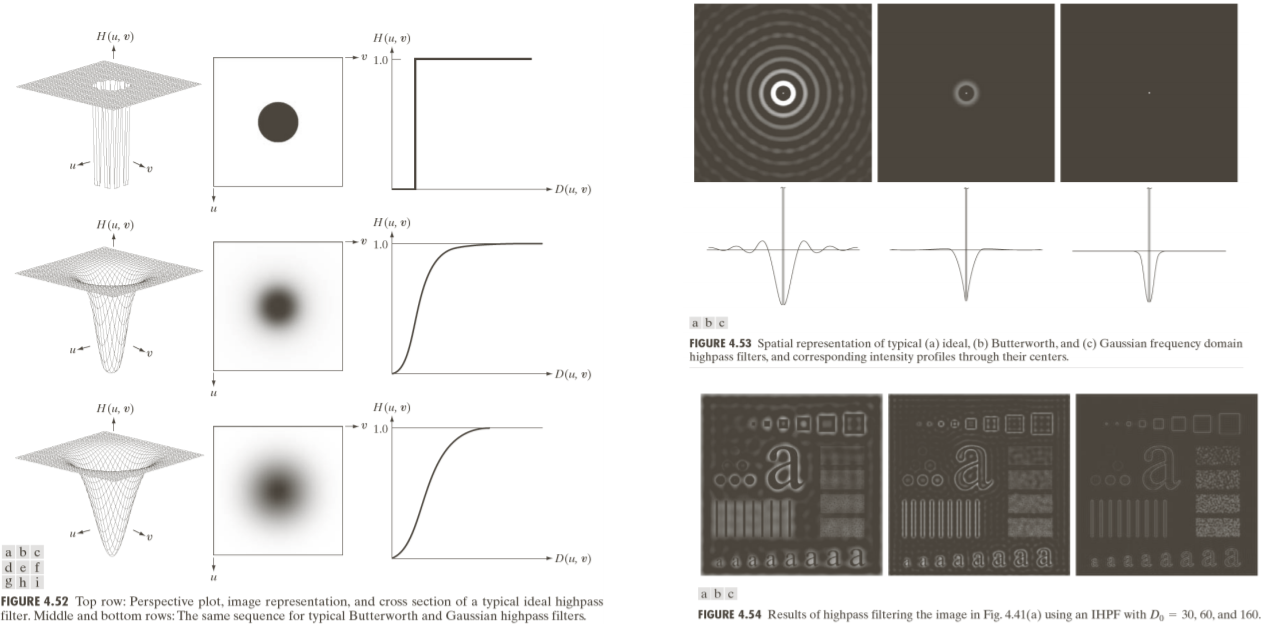
Highpass filter <-> Lowpass filter
Lowpass filter는 가운데를 통과시키고 나머지는 다 0이 된다.
Highpass filter는 그 반대이다. 어떤 프리컨시 이상만 살린다.
ideal highpass filter는 ringing effect가 생긴다.
butterworth의 경우는 좀 덜하지만 그래도 ringing effect가 생기긴 한다.
gaussian의 경우에는 ringing effect 발생 X
highpass filter만 통과시키면 에지나 텍스쳐만 살아남고 나머지 부분은 제거된다.

위 사진은 highpass filter를 통해 선명해졌다.
4. 이미지 프로세싱
1) Color fundamentals
- brightness : 인텐시티의 밝기
- hue : 주요 컬러. 색조
- saturation : 채도. 그 색조가 얼마나 순수하게 차지하는지, 얼마나 선명한지
- chromaticity : hue & saturation
2) RGB color models
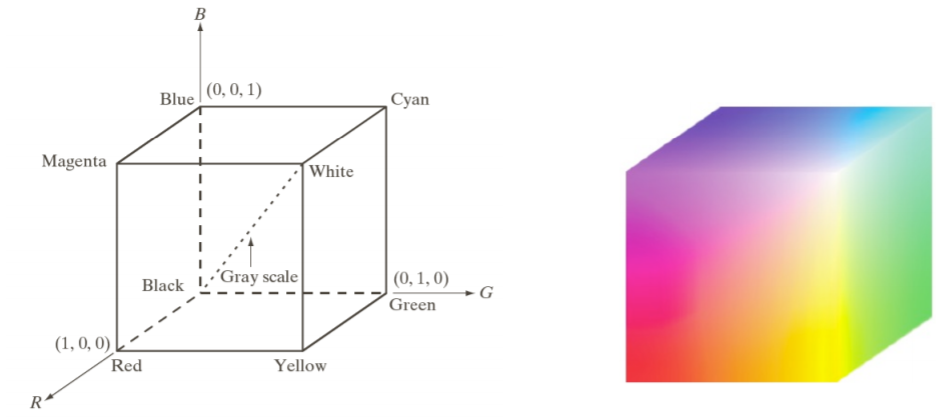
앞에서 설명한 기존의 gray level에서는, 8비트를 사용한다고 할 때, 2^8 = 256
black과 white를 0~255 사이로 quantization을 해서 사용하는 1-channel intencity를 사용했다.
그런데 color를 표현하기 위해서는 RGB. 3채널 사용한다.
검정색이 origin을 나타낸다.
3) CMY & CMYK color models
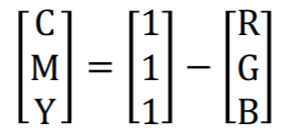
실제로 프린트를 하게 될 때는, 1에서 RGB를 뺀 transform을 거쳐서 CMY 모델을 만든다.
or 검정색을 표현하기 위해서 검정색을 합친 CMYK 모델을 많이 사용한다.
4) HSI color models
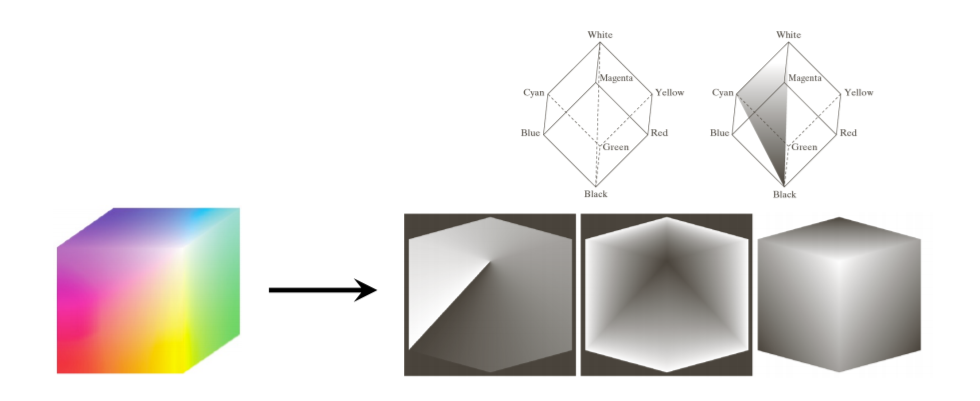
RGB나 CMY같은 경우, color 모니터나 프린터를 할 때 사용되지만, 실제로 사람이 표현하는 데는 많이 실용적이지는 X
우리는 이것을 HSI color models을 사용해서 좀 더 사람이 표현하는 것과 비슷하게 표현할 수 있다.
이때는 hue, saturation, brightness. 이 3가지 축을 이용해서 color를 표현한다.
H S I
HSI는 the color-carrying information에서 the intensity component를 분리한다. 그리고 이미지 처리에 이상적이다.
5) Pseudo color image processing
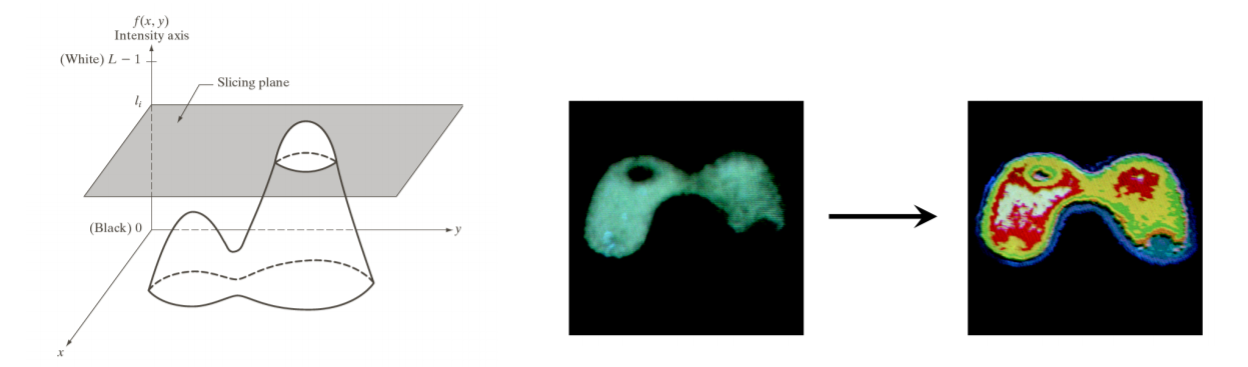
기존의 gray로 표현되었던 것들을 좀 더 visualization하고, 분석하기 좋도록 pseudo color를 사용한다.
intensity에 따라서 서로 다른 색을 주게 된다면, 눈으로 봤을 때 어떤 부분이 어떤 intensity를 갖는지 쉽게 알 수 있다. (= Intensity Slicing)
6) Perform three independent transforms
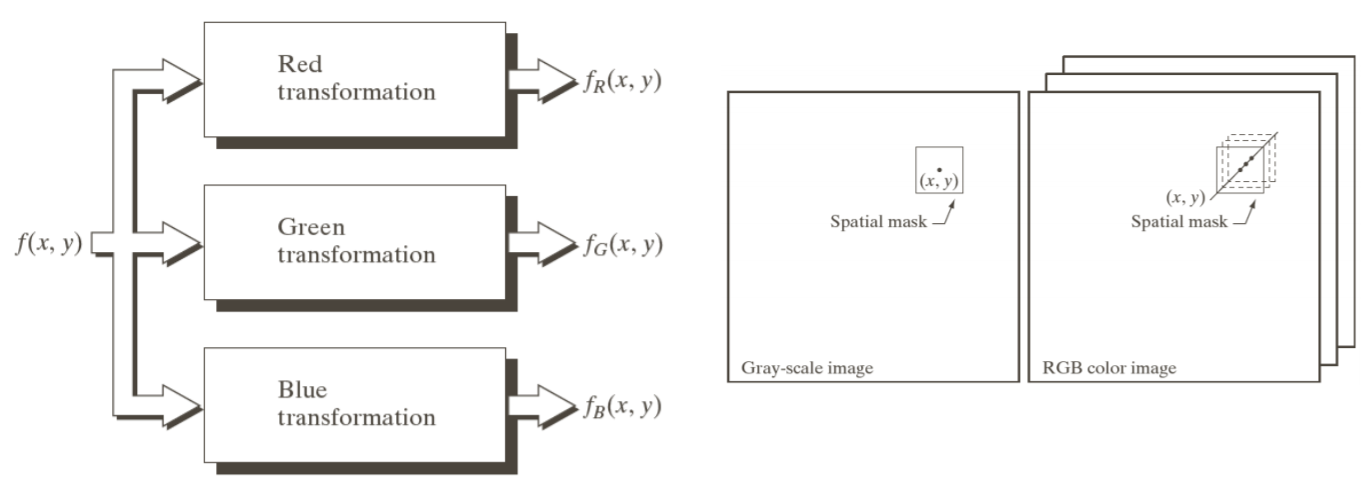
기존 gray 1 channel로 프로세싱한걸 컬러 이미지에서는 3채널이 생긴다.
그리고 각 채널에 따라서 독립적으로 수행된다.
7) Perform color image processing
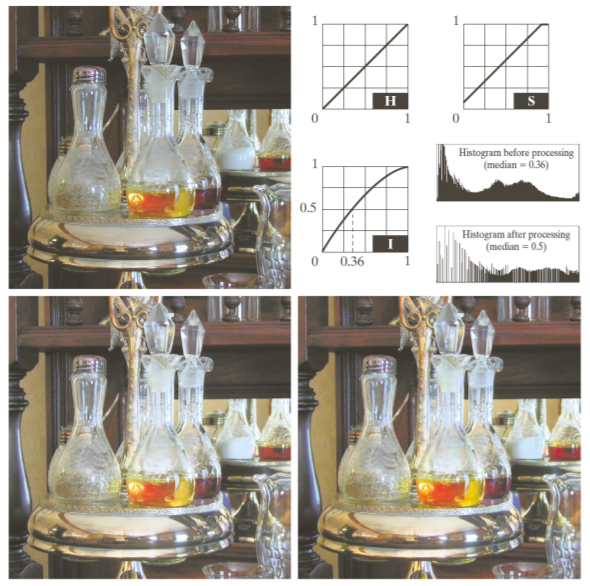
컬러 이미지 프로세싱을 통해 영상을 더 밝게 보정한다던지 필터링을 한다던지 등 할 수 있다.
'전공 > 컴퓨터 비전' 카테고리의 다른 글
| [컴퓨터 비전] Introduction to Deep Learning (0) | 2021.04.20 |
|---|---|
| [컴퓨터 비전] Neural Networks and Backpropagation (0) | 2021.04.18 |
| [컴퓨터 비전] Linear Regression and Logistic Regression (0) | 2021.04.14 |
