<TOPIC>
• Linear Regression
- What is Regression?
- Regression Function
- Linear Regression
- Cost Function for Linear Regression
- Gradient Descent
• Logistic Regression
- What is Classification?
- Classification Function
- Logistic Regression
- Cost Function for Logistic Regression
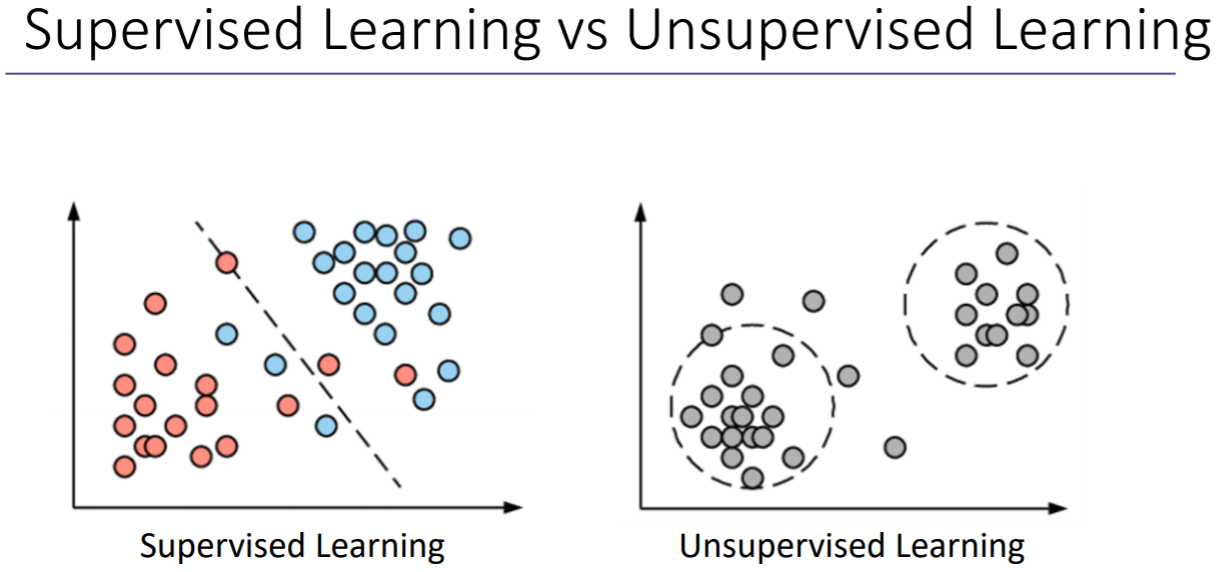
위 그림에서 Supervised Learning은 빨간색, 파란색 레이블을 어떻게 나누면 될지 선을 찾아주면 되고, Unupervised Learning은 아무런 레이블 없이 분포하는 것을 알 수 있다. 그래서 데이터만 보고 적절하게 어떤 클래스에 있는지 찾아낸다.
- Supervised Learning(지도학습) : 정답이 있는 데이터를 이용한 학습 방법 <- 로지스틱 회귀, 리니얼 회귀 해당
- Unupervised Learning(비지도학습) : 정답이 없음
1. Linear Regression
1) What is Regression?

depth estimation은 깊이 정보를 추정하는 기술을 말한다. 이는 추정하는 값들이 연속적인데, 이와 같은 것을 regression이라고 한다. semantic segmentation 영상을 의미론적으로 서로 다른 부분들을 분할해내는 것을 말한다. 이렇게 어떤 클래스에 있는지 discrete한 카테고리를 찾아내는 것을 classification이라고 한다.
logistic regression이 binary로 설정되기때문에 어떤 classification을 logistic regresson으로 수행한다.
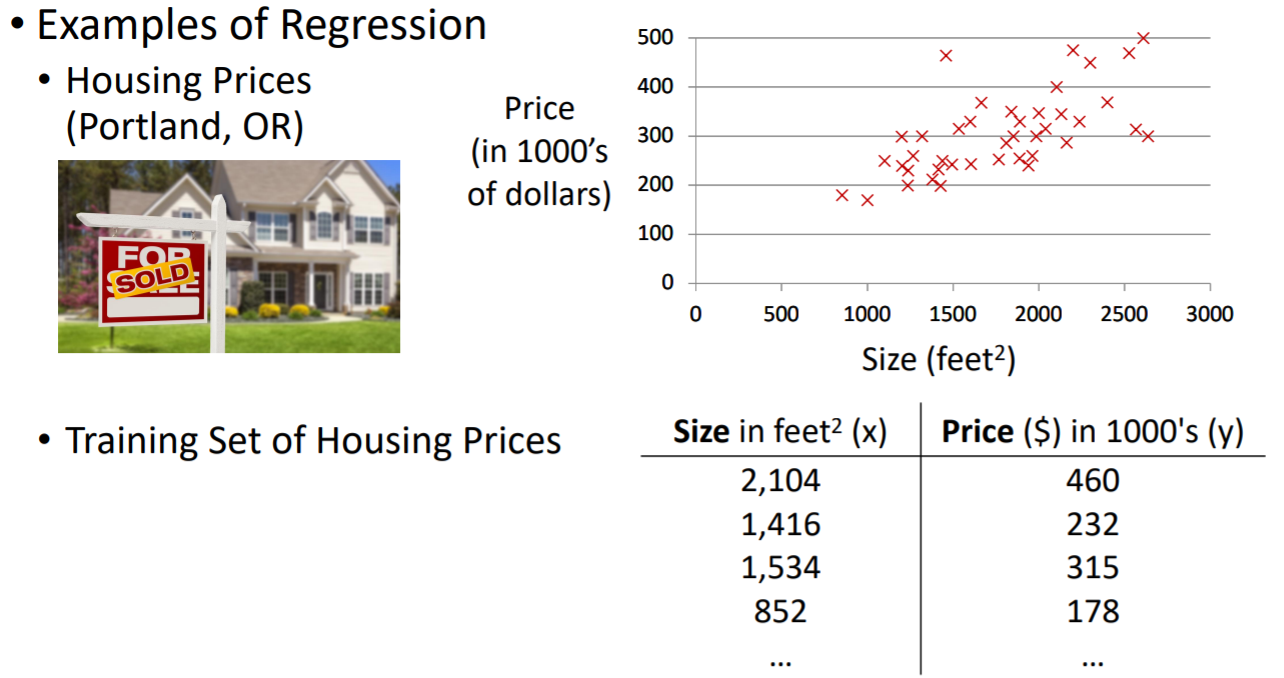
Regression은 데이터를 이용하여 사이즈와 프라이스가 어떤 관계인지 찾는 것이다.
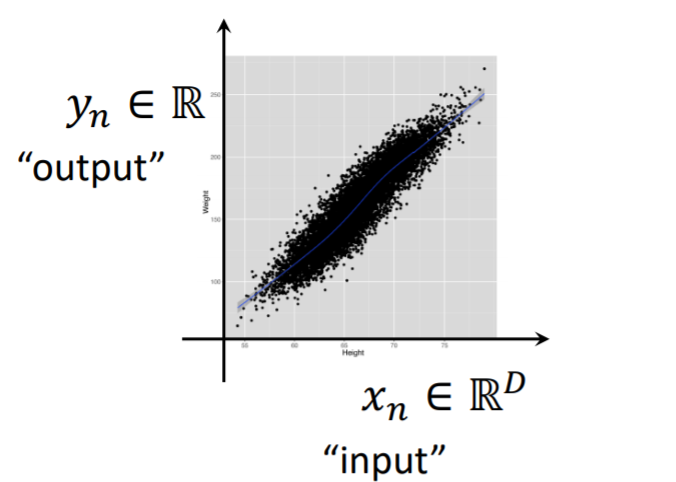
즉 Regession은 인풋 변수와 아웃풋 변수를 이용하여 새로운 인풋에 대한 아웃풋을 예측하고, 아웃풋에 대한 인풋이 어떤 효과를 주는지 예측하는 것이다. D라는 디멘션을 가진 인풋을 가지고 어떤 실수값 y를 예측한다. Regession의 경우는 이렇게 아웃풋이 continuous한 값을 갖는다.
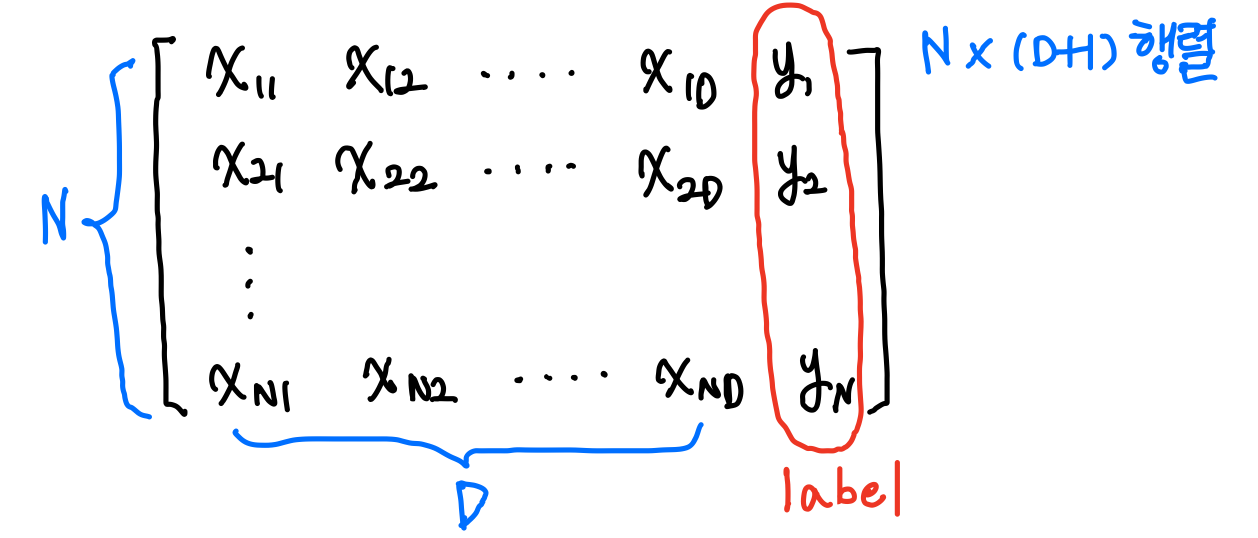
Regession은 데이터셋은 항상 인풋과 아웃풋 pair로 존재한다. 그리고 위와 같이 pairs의 수인 N은 데이터셋의 크기와 같다. 그리고 D는 dimensionality이다.
☞ Machine Learning Term for Regression
- Input variables
= features = covariates = independent variables = predictors, etc.
- Output variables
= target = label = response = outcome = dependent variable = measured variable, etc.
Regression의 목적은 2가지가 있다. 먼저 인풋에 대한 결과 예측하기 위함이고, 인풋이 아웃풋에 어떤 영향을 미치는지 분석하기 위함이다. 그 예시로는 10년 넘게 흡연하는 자의 수명 예측, 흡연이 암 유발하는지, 캘리포니아에서 30년안에 큰 규모의 지진이 발생할지 등이 있다.
2) The Regression Function (Hypothesis)
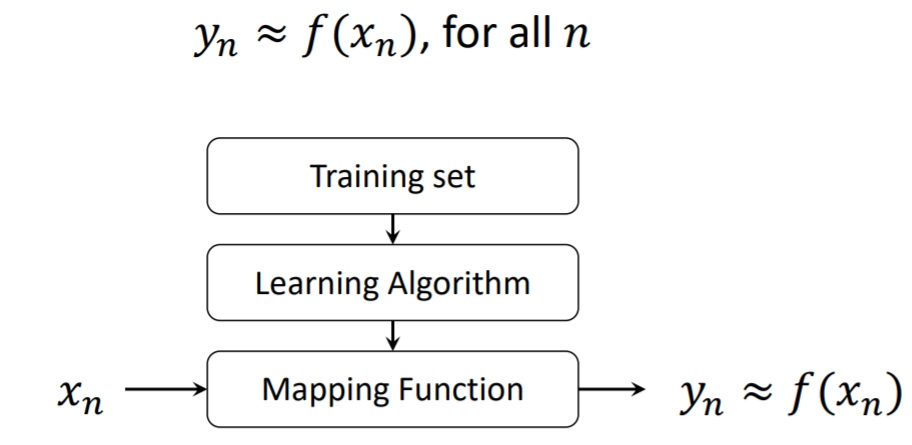
주어진 인풋을 잘 예측하게 하는 매핑 함수를 찾는 것이 리그레션의 목표이다.
찾고자하는 매핑 함수를 f(xn) 이라고 하자. 매핑 함수를 통해 xn이라는 인풋이 들어갔을 때, 아웃풋이 f(xn)이고, y와 최대한 유사한 f(xn)을 찾는 것이 목표이다.
3) Linear Regression
Linear Regression은 인풋과 아웃풋의 선형적인 관계를 갖는다. 우리는 인풋과 아웃풋 사이의 straight line을 찾고자한다. 참고로 non-linear한 경우, yn = xn^2, yn = x1x2 ... 와 같은 경우이다.
주로 많은 Regression에서 linear를 가정하고 푼다. 왜냐하면 더 간단하기 때문이다. 이 밖에도 이해하기 쉽고, 식이 풀기 편하고, 논리니어 모델에 대해서도 훨씬 generalization이 잘된다는 장점이 있다. 우리는 Linear Regression만 잘 이해해도 많은 데이터의 관계를 알게 된다. 실제로 Linear Regression 기반으로 많이 이루어져있다.

D=1일때를, Simple linear regression이라고 한다.
파라미터를 이용해서 선형관계를 찾게 되고, 기울기를 찾아서 직선을 찾아낸다.

데이터가 주어질 때, 데이터들의 관계를 가장 잘 설명할 수 있는 최적의 파라미터 w를 찾아내는 것이 목표이다. 이 과정을 러닝 또는 'estimationg the parameters or fitting the model' 이라고 한다. 그러기 위해서는 optimization algorithm을 이용한다.
4) Cost Function for Linear Regression
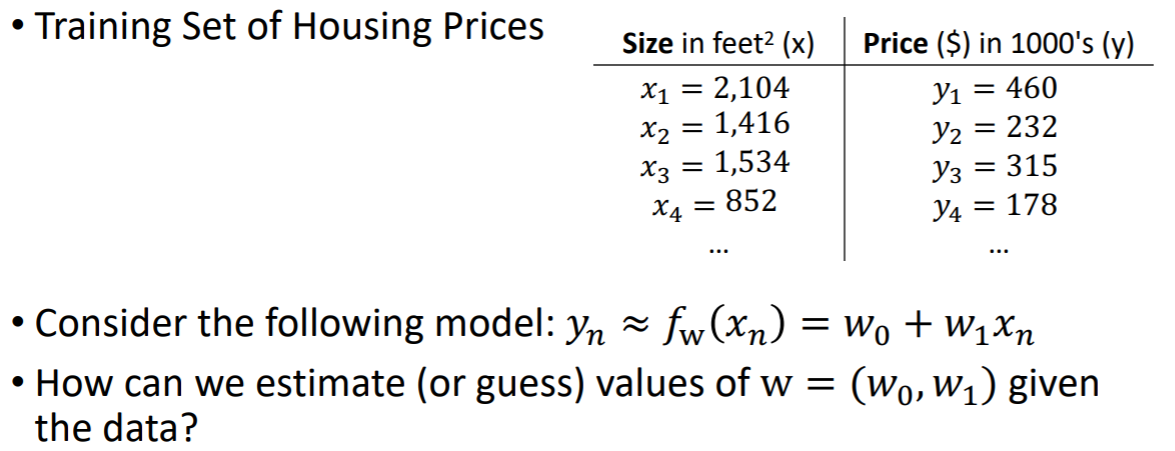
위 예시에서는 size가 인풋 x, price가 아웃풋 y이다. 그리고 적절한 파라미터를 찾아서 매핑 함수를 찾아낸다. 이 때, 매핑 함수가 실제 y와 최대한 유사한 값을 가지도록 매핑함수를 찾아내야한다. 여기서 yn이 정답이 되기 때문에, ground-truth 이라고 표현한다. 매핑 함수를 통해 나온 값인 fw(xn)은 estimation된 값이다.
이 데이터를 이용해서 어떻게 w를 예측해야할까?
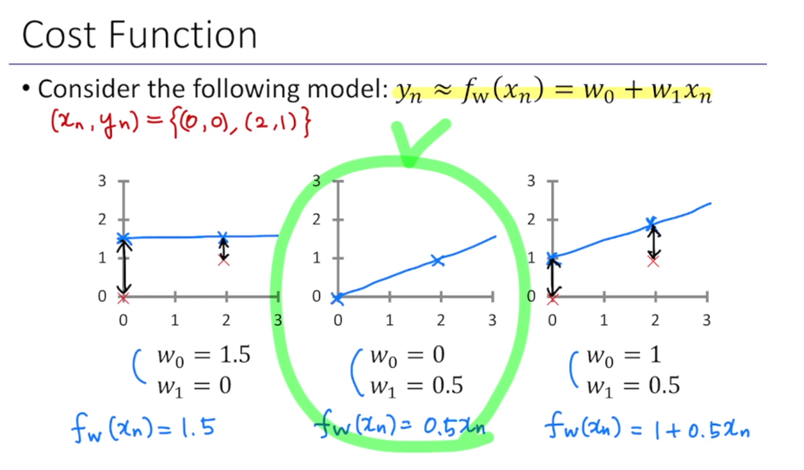
세 그래프에서 표시된 검은색 화살표가 에러를 나타낸다. 이를 보고 판단하면, 가운데의 경우가 가장 에러율이 적고 제일 xn, yn이 잘 fitting되어있는 것을 알 수 있다.
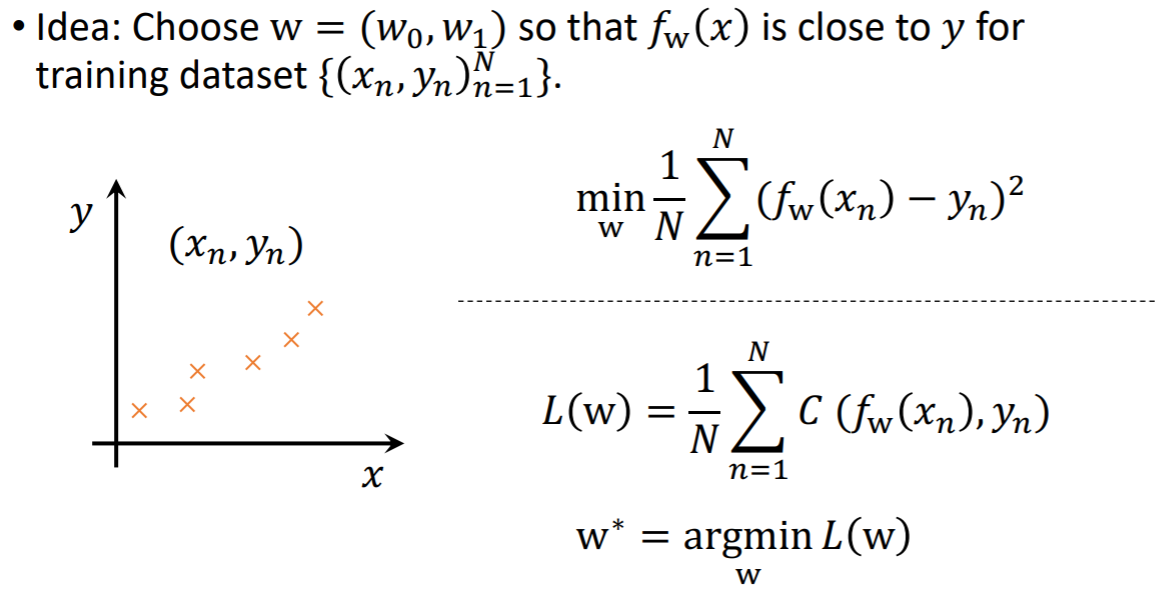
비용 함수는 우리가 설계한 모델 or 매핑 함수가 얼마나 데이터를 잘 설명하는지 측정하는데 사용된다. 또는 에러가 얼마나 존재하는지 측정하는데 사용된다.

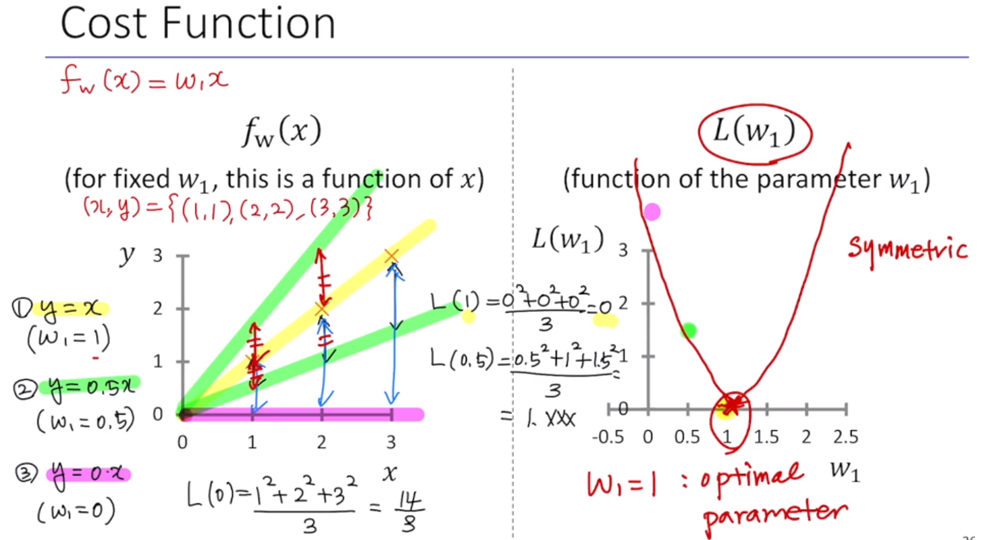
위에 따르면, y = x일 때 가장 잘 맞게 fitting됨을 알 수 있다.
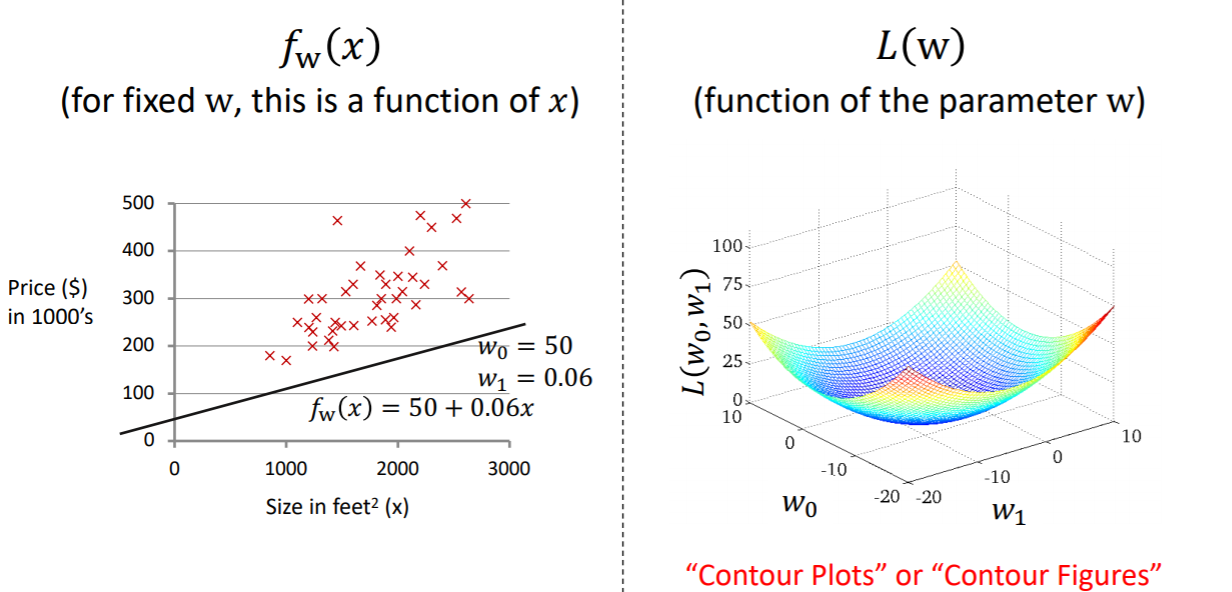
위는 w0과 w1에 대한 함수이기 때문에 3차원 공간상에 표현된다. 이는 coutour plot 또는 contour figures라고 불린다.
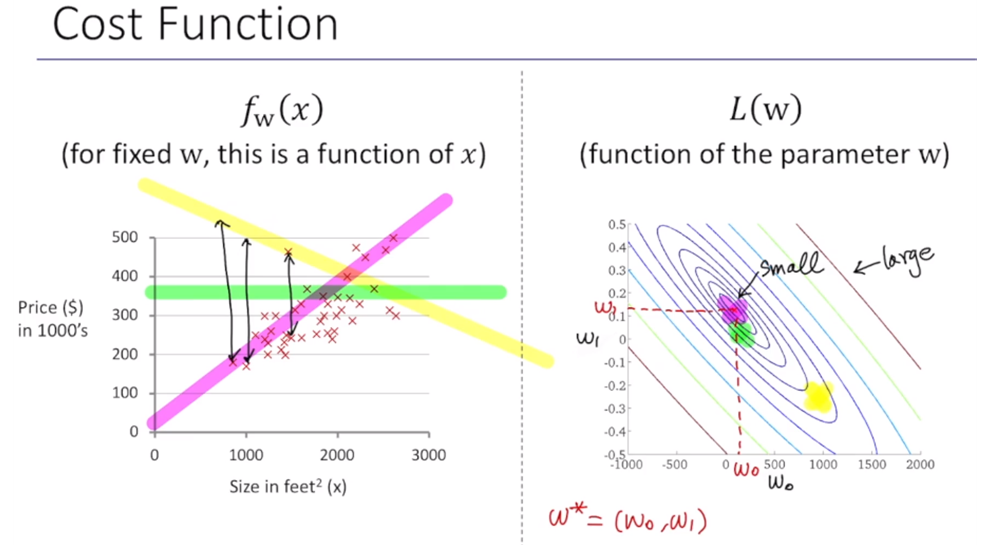
에러들의 sum = cost 이라고 이해하면 된다. 그리고 오른쪽 그래프에서 보라색 점이 우리가 찾고자 하는 파라미터 w*이다. 이렇게 2차원상에 표현하면, 일반적으로 이렇게 컨투어 형태로 표현된다. 이게 멀어질수록 cost가 커진다(large).
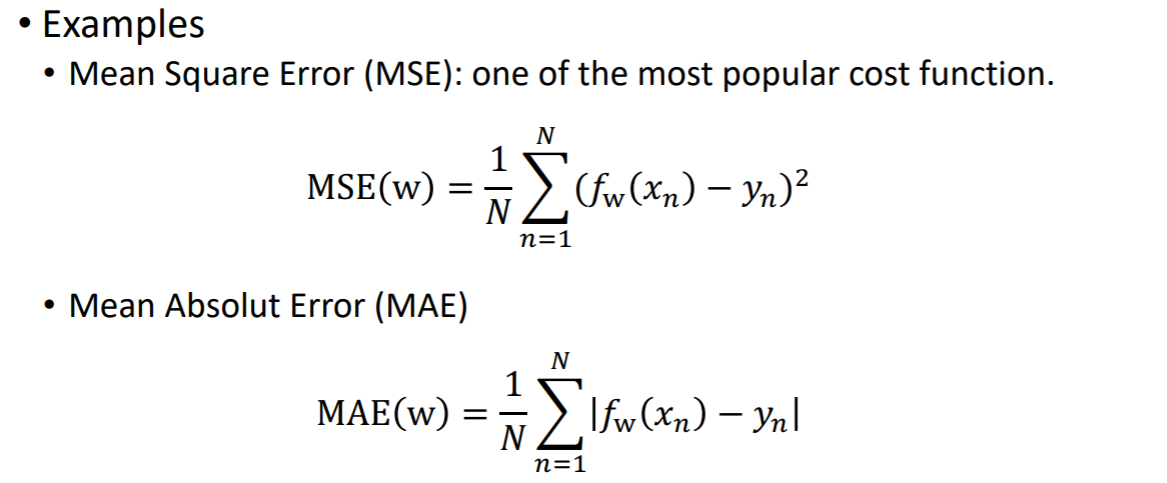
이전 포스팅에서 정리한 내용으로, 에러의 제곱의 평균을 cost 함수로 썼었다. 이 밖에도 다른식으로도 코스트 함수 쓸 수 있다. MSE는 가장 많이 사용된다. MAE는 실제 아웃풋과의 절대값을 이용해서 그 절대값들의 평균을 cost로 사용한다. 데이터에 따라 달리 사용된다.
그럼 비용함수가 어떤 특성들을 가지면 좋을까?
cost는 0을 중심으로 symmetric한게 좋다. → 그 이유는 에러가 positive하거나 negative일 때도 똑같은 에러만큼을 페널티를 주는 것이 좋기 때문에 symmetric한 성격을 갖는 것이 좋은 비용함수이다.
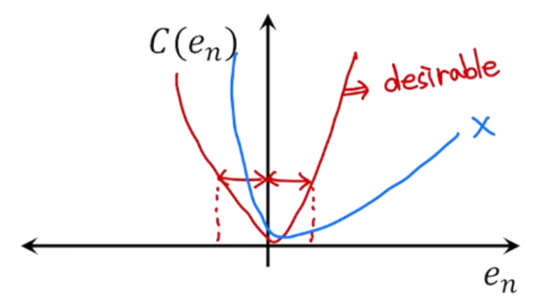
빨간색 : 좋은 비용함수
파란색 : 좋지 않은 비용함수
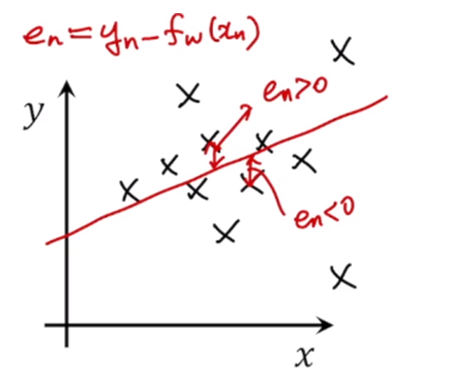
y가 더 큰 경우 양수, 더 작으면 음수
같은 양만큼 페널티를 줘야하기 때문에 symmetric한게 좋은 비용함수이다. 그리고 큰 에러 또는 매우 큰 에러에 대해 같은 페널티를 주도록 비용함수를 설계하는게 좋은 비용함수이다.
에러가 발생하게 될 때, 너무 큰 cost를 주면 에러를 작게 하는 파라미터를 ~하기 때문에 이 값들을 줄이기 위해서 function이 파라미터가 잘못 구해질 확률이 있다. <- 보충필요!
그래서 모여 있는 데이터들에 대해 잘 fitting시키는 function이 필요한데, 너무 큰 에러에 대해 너무 큰 cost를 줘버리면 파라미터가 잘못 구해질 확률이 있다.
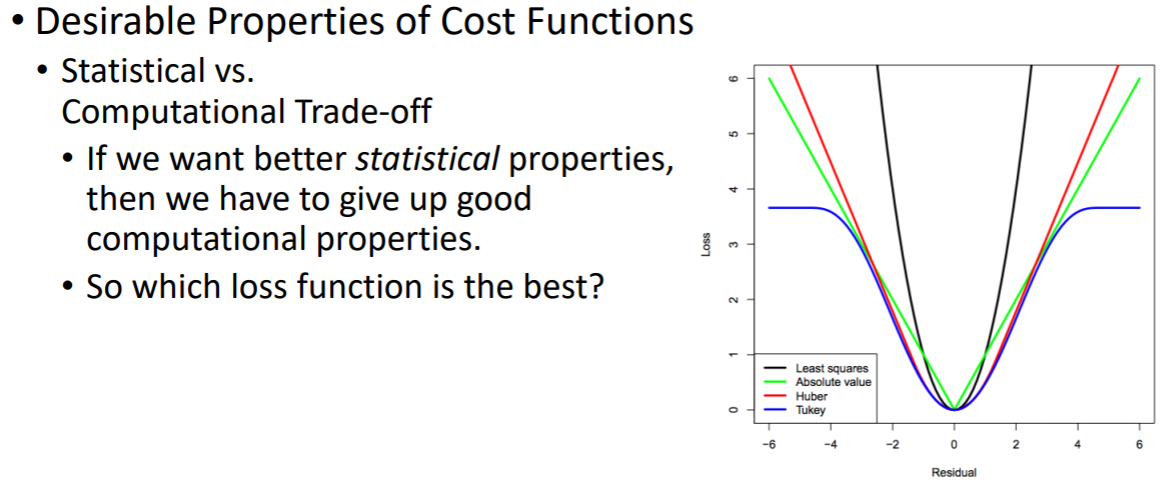
검은색 그래프는 MSE, 초록색 그래프는 MAE
노란색 – 1) 시멘트릭하고 2) 어느정도 에러가 커지면 같은 값을 줌으로써 너무 큰 에러에 대해서도 그 파라미터가 그 에러 를 줄이기 위해 치우치지 않도록함
근데 가장 많이 사용하는 것은 MSE(가장 좁은 모양)이다. → 실제로 구현하기도 쉽고 최적화하는 게 제일 편하기 때문
좋은 비용함수에 대해서는, computational complexity가 높아진다는 단점이 있기 때문에 trade off가 생기게 돼서 어떤 loss function이 가장 좋냐? 는 질문에는 사실 알 수가 없다. → 어떤 데이터마다 최적의 로스 함수가 모두 다르고, 사용하고자하는 복잡도를 만족해야하고 어느정도까지 에러를 수용할지 다 다르기때문이다.
그래서 데이터마다 적절한 코스트 메트릭을 이용해서 로스 함수를 정의하면 된다.
5) Gradient Descent
어떤 비용함수 L(w)에 대해 최적의 파라미터 w*를 찾는 방법은?
이전에는 w를 변화시켜가면서 매핑 함수와 실제 아웃풋간의 차이를 통해 코스트를 계산했었다.
grid search는 모든 w에 대해 비용을 계산하고, 그 중에서 비용이 가장 작을 때의 파라미터를 선택하는 방법이다. 이는 매우 단순하지만 실제로 브루트포스하고, 모든 w에 대해 수행하기 때문에 복잡도가 매우 높다는 단점이 있다.

그래서 우리는 gradient descent라는 방법 사용해서 grid search보다 낮은 복잡도로 w*를 찾을 수 있다. 내려가는 방향으로 계속 이동하다보면 맨 아래점까지 도달 가능하다. 이런 식으로 gradient descent는 이런 컨투어가 있을 때 여기서 minimum한 지점을 가고자할 때, gradient가 낮아지는 방향으로 계속 따라가다보면 미니멈에 도달한다는 방법이다.
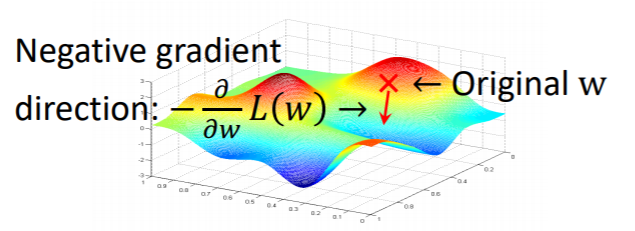
비용함수가 이렇게 존재할 때, 여기서 찾고자하는 것은 minimum한 곳까지 어떻게 도달하는지는, 경사를 계속 내려가면서 그레디언트를 구해주는 방법을 반복하면 미니멈에 도달하게 된다. 그래서 gradient descent는 어떤 포인트에서 gradient를 찾아주게 되고, 그 방향으로 계속해서 더해주게 됨으로써 minimum을 찾아가면 된다. 이때 방향은 점점 내려가기 때문에 negative gradient가 되어야한다.
initial point는 어떤 시작점 w=(w0, w1)에서 시작하여, L(w)를 줄이는 방향으로 w를 계속해서 업데이트해준다.
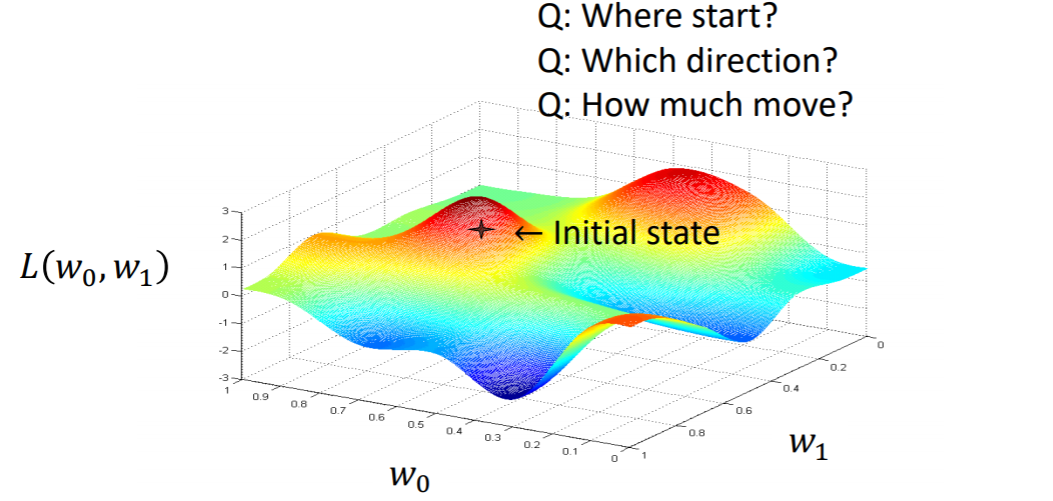
Q. initialization을 어떻게 줘야할까? -> gradient로 줄 것임
Q. 어떤 방향으로 줘야할까?
Q. 얼마나 움직여야할까? -> learning rate
어떤 시작점 initial state에서 negative gradient쪽으로 점점 내려간다. 이 때, 얼마만큼 내려올지 결정하는 것이 learning rate이다. 계속 이 동작을 수행하다보면 미니멈에 도달할 수 있게 된다.

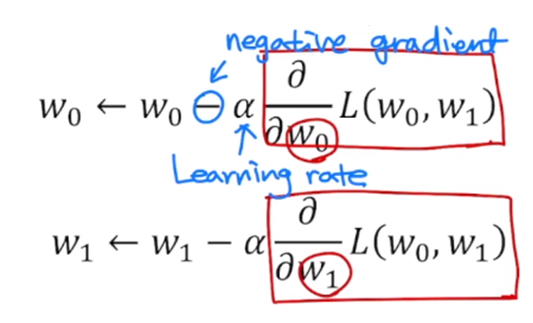
임의의 한 점에서 시작하여 w0에 대해 partial gradient를 구해주고, w1에 대해 partial gradient를 구해준다.
그러면 여기에서 적절한 learning rate α를 곱해서 그 방향만큼 계속 업데이트해준다.
그리고 w0에 대해 negative 방향으로 빼준다.
이런식으로 w0, w1을 업데이트한다. 그렇게 convergence까지 계속 반복 수행한다.
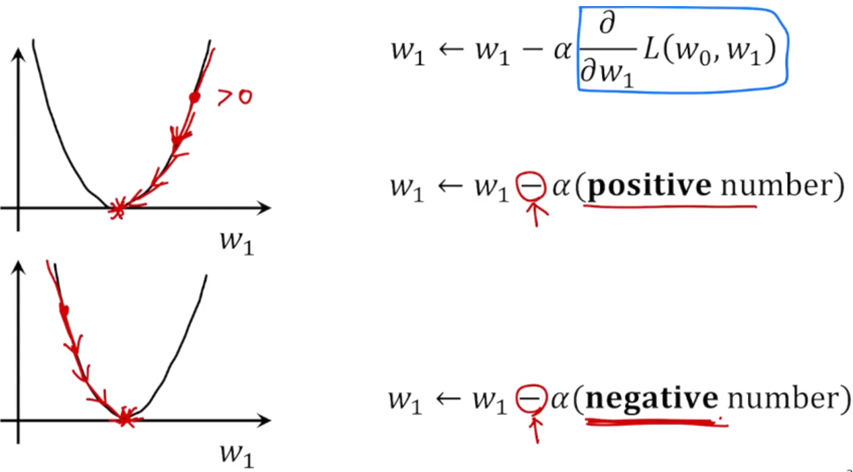
positive나 negative나 상관 없이 곱한 gradient의 음수방향으로 업데이트하게 해주면 결국 mininum 도달할 수 있다.
러닝 레이트는 어떤 역할을 할까?
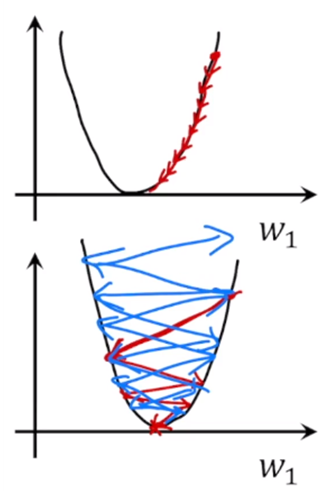
내려오는 크기를 얼만큼 내려올지 정하는게 learning rate인데, 만약 learningrate가 너무 작으면 convergence까지 내려오는게 너무 느려진다. 반대로 learning rate가 너무 크면, 한 번에 너무 많이 가기 때문에 반대쪽으로 갈 수 있다. 지그재그 모양이 가능하다.
만약 이니셜 포인트가 0이라면, ?까지 왔다가 더 이상 그레디언트가 0이 돼서 거기서 수렴이 되어버린다. //보충필요!
가장 낮은 부분을 global minimum이라 하고, global minimum은 아니지만 낮은 값을 local minimum이라고 한다.
우리는 global minimum을 찾는게 목표인데, 출발을 어디에서 하느냐에 따라 local minimum에 빠져버리는 것이 gradient descent의 한계이다. 즉, 항상 어떤 시작점에 대해서도 global minimum에 도달하지 않는다는 한계가 있다.
여기까지는 D=1인 경우를 살펴봤다. 이제는 D=N으로 확장할 경우, 어떤 매핑 함수를 가지는지 살펴볼 것이다.
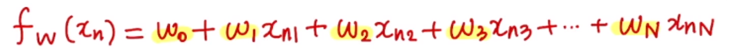

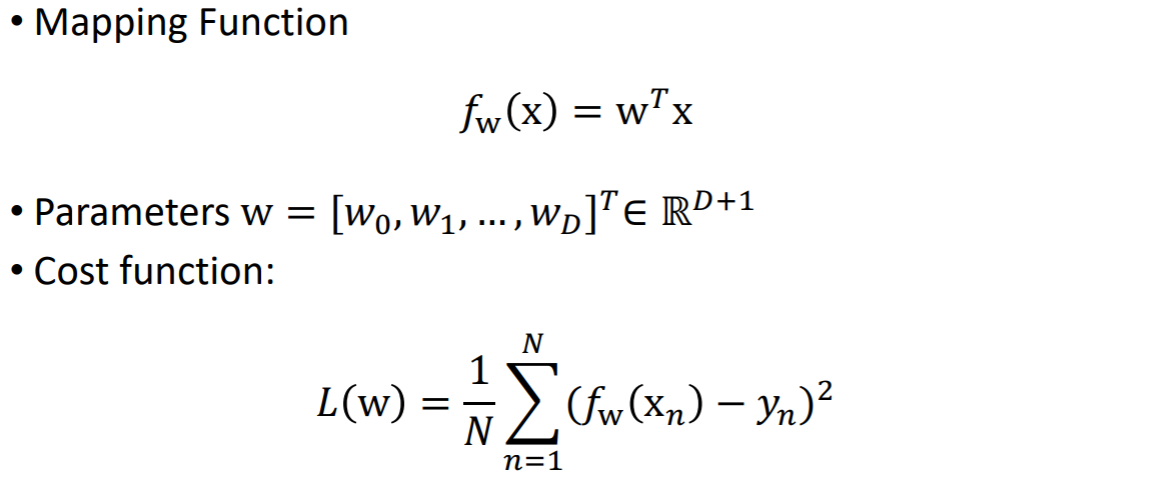
MSE를 가정할 때 위와 같이 cost function을 나타낼 수 있다.

위는 single variable과 multiple variables의 차이를 나타낸다.
single variable → w0, w1을 찾는 것
이 때 구하고자 하는 w*= [w0, w1]
비용함수를 각각의 원소로 partial derivative해서 gradient descent 방법을 이용해서 파라미터를 업데이트한다.
multiple variables → i가 0에서 n까지의 값을 가짐
각각을 wi에 대한 partial derivative를 구해서 wi를 업데이트
위 식은 MSE를 가정하고 wi에 대해 미분하여 마지막 식을 얻었다.
이렇게 모든 wi가 어떤 일정한 값으로 수렴할 때까지 이 과정을 계속 반복한다.
2. Logistic Regression
1) What is Classification?
linear regression → continuous한 아웃풋을 구하는 것
logistic regression → 그 값이 continuous하지 않고 binary로 결정됨
Regression과 비슷하게, Classification는 인풋 변수 x와 아웃풋 변수 y를 연관시킨다. 그러나 Classification은 discrete한 카테고리를 찾는 것이다. y가 discrete한 값을 갖는다는 것이 가장 큰 차이이다. 그래서 y는 더 이상 continuous한 값이 아니고 categorical한 값이다. y는 categorical variable이라고 불린다.
예를 들어, 어떤 이메일이 스팸이냐 or 스팸이 아니냐?
양성 종양인지 악성 종양인지 판단할 때 등이 있다.
-> 2가지 카테고리로 나뉨

그런데 linear regression으로 설계하면 모두 0으로 존재하는 데이터에 대해서 에러가 발생한다. 에러의 크기가 다르다. y=1로 예측해야하는 경우에도 에러의 크기가 점점 달라진다. 에러가 모두 같은 양을 가지면 좋은데, 페널티가 달라지기 때문에 이런 경우에는 좋은 비용함수라고 볼 수는 없다.
y가 0~1사이에 존재한다는 ?가 있기 때문에 이런 classification에 적절한 매핑 함수를 새롭게 설계 가능하다. 아웃풋 y가 항상 0~1 사이에 존재하기 때문에 매핑 함수를 0과 1로 정규화한다. 그리고 0과 1사이의 값에서 threshold값을 0.5로 해서, 0.5보다 크면 1에 가깝게, 0.5보다 작으면 0에 가깝게 다음과 같은 매핑 함수를 새롭게 설정한다.
이렇게 생긴 매핑 함수를 정의해보자면, 0에 대해 같은 패널티, 1에 대해서도 같은 패널티를 갖는다. 이 사이의 영역에 존재하는 데이터들은 불확실한 값을 갖는다. 이런 매핑 함수를 설계하게 된다면, classification에 적합한 함수라고 볼 수 있다.
2) The Classification Function (Hypothesis)
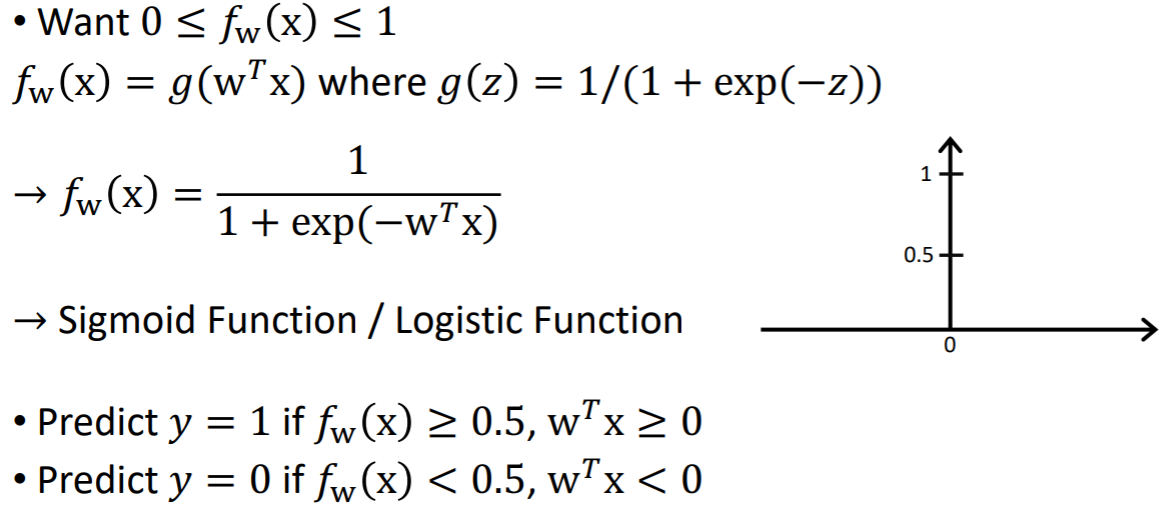
실제 y값이 0과 1사이에 존재하기 때문에 매핑함수값 fw(x)도 0과 1사이에 존재한다.
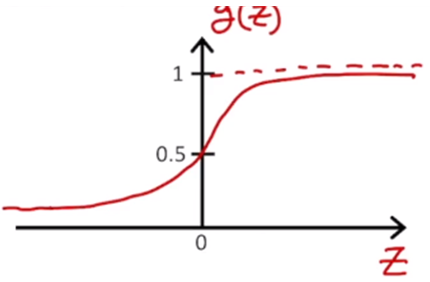
시그모이드 함수(로지스틱 함수)를 사용해보면, 어떤 인풋에 대해 0보다 크면 0.5보다 큰 값을 가지게 되고, 0보다 작으면 0.5보다 작은 값을 가지게 된다. 이 함수를 이용해서 classifcation의 비용함수를 정의할 수 있다.
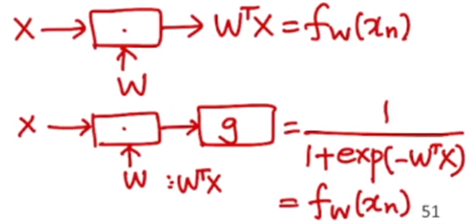
기존의 regression에서는 인풋 x에 대해 적절한 파라미터 w를 곱해줘서 위와 같은 매핑 함수를 설계했었다.
이제 classification에서는 절절한 파라미터 w를 곱해준 후에, 시그모이드 함수를 이용하여 매핑 함수를 가진다.
classification은 logistic regression이라고도 불리운다.

0<= fw(x) <= 1이기 때문에, 확률적인 관점에서 살펴볼 수 있다.
fw(x) : x가 있을 때 항상 y=1일 확률
→ 조건부확률로 나타내기 가능
y=0일 확률과 y=1로 확률의 합은 항상 1이다.
fw(x) = 0.7 이라는 것 → 악성일 확률이 70%, 악성이 아닐 확률이 30%라는 것과 동일한 의미
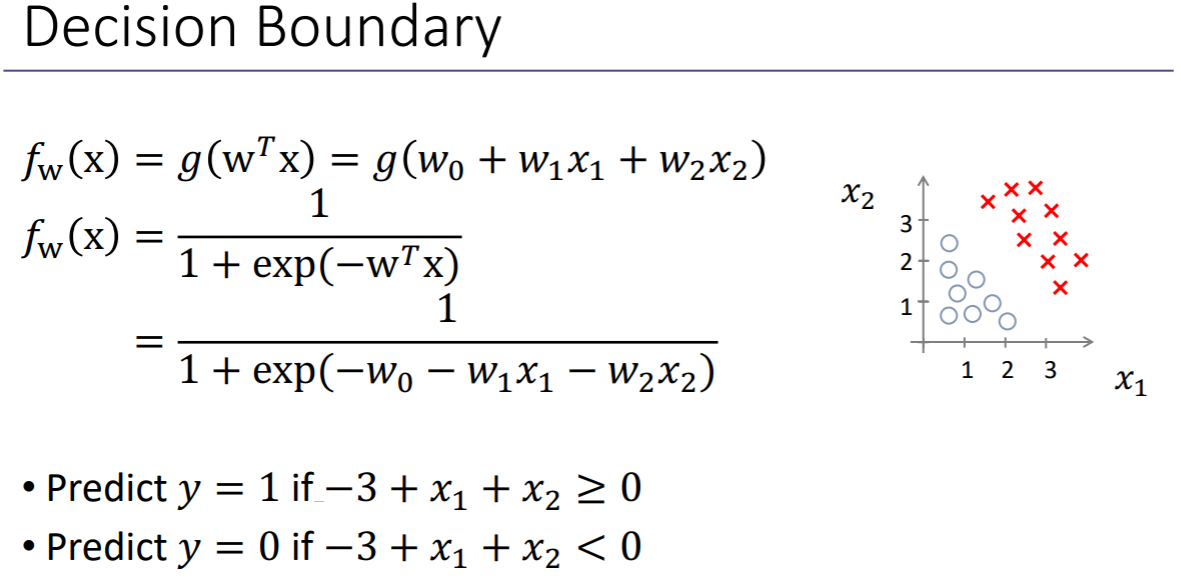
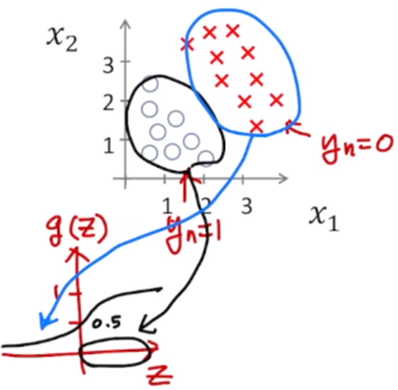
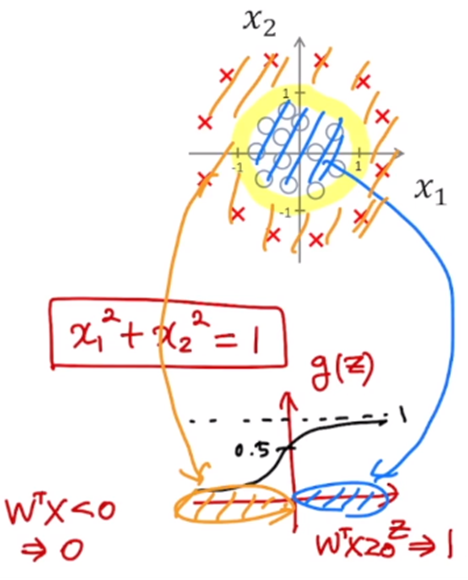
classification에서는 decision boundary라는 개념이 있다. 구분할 수 있는 경계선이다.
x1 + x2 – 3 = 0 → x2 = -x1 + 3
이 바운더리보다 작으면 y = 1로 예측 ← wTx >= 0
이 바운더리보다 크면 y = 0으로 예측 ← wTx < 0
-3 + x1 + x2 = 0 : decision boundary
x1, x2사이에서 각각을 선형으로 decision boundary를 정의한다.

3) Logistic Regression
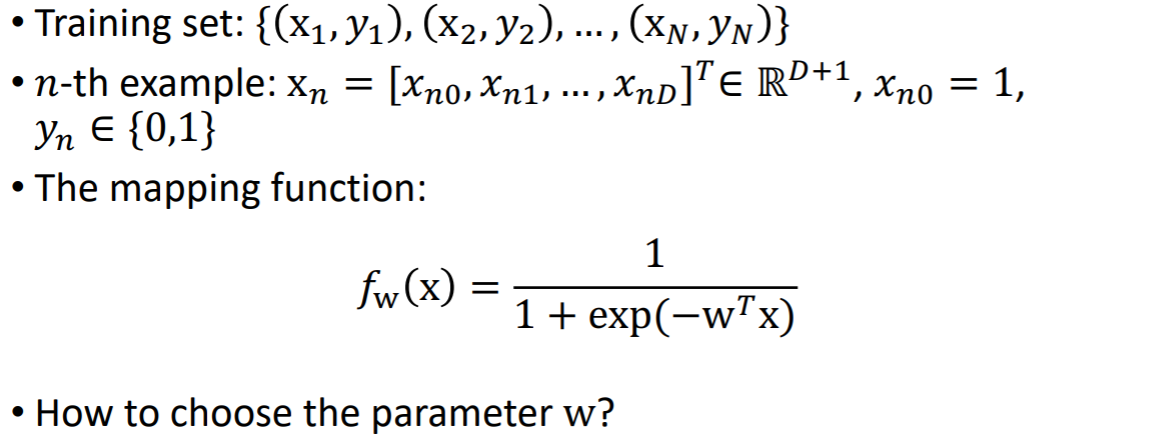
4) Cost Function for Logistic Regression
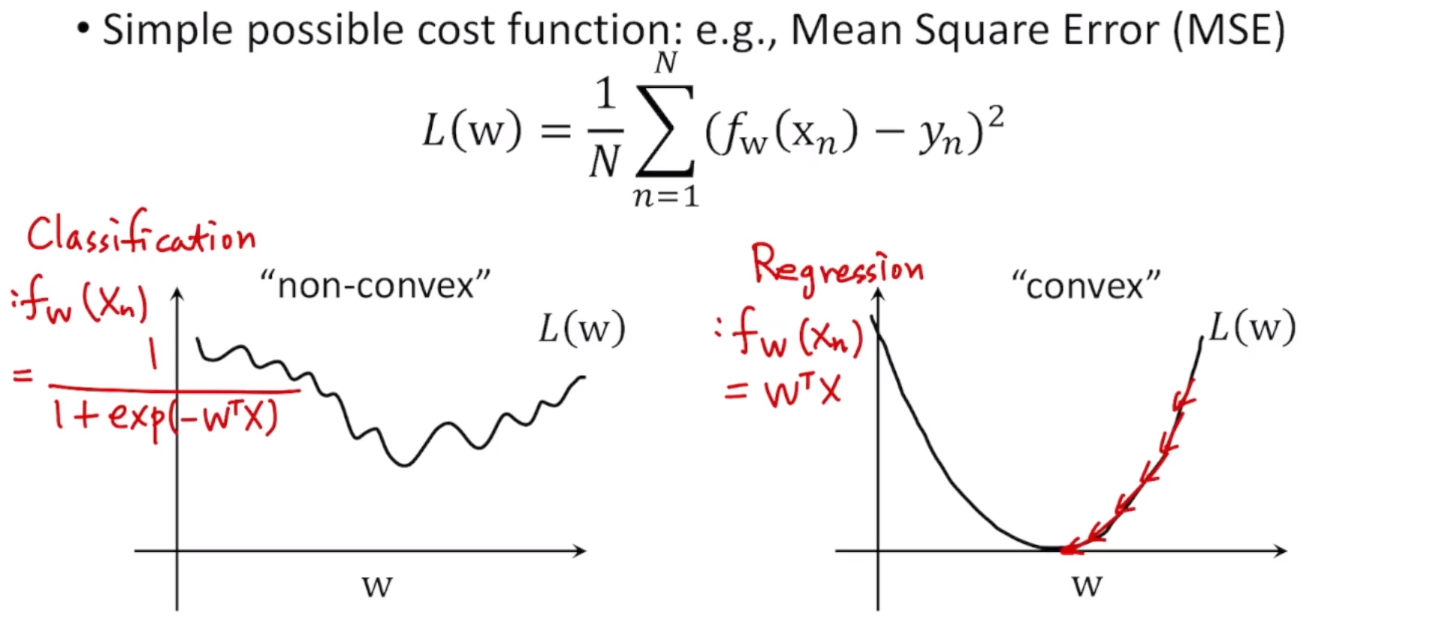
linear할 경우, fw(xn) = wTx 이므로, 비용함수가 오른쪽 그래프의 모양으로 컨벡스 형태로 나온다. 여기서 gradient descent를 하게되면 global minimum을 찾는다.
classification의 경우 fw(xn) = 1 / (1+ exp(-wTx))이다. 그래서 왼쪽 그래프의 모양으로 non convex(물결 모양)한 형태가 나온다. 이런 경우에 w에 대해 gradient descent를 수행하면, local minimum에 빠지기 때문에 global minimum을 찾기 쉽지 않다. 그래서 이런 경우에는 적절한 비용함수가 아니다.
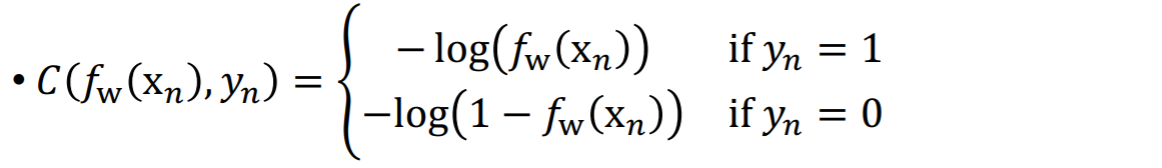
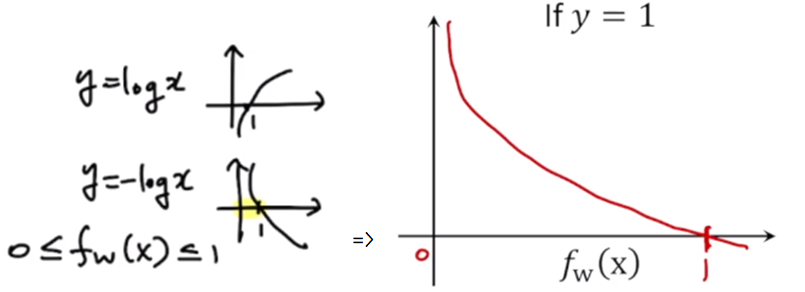

0에서 1사이에 존재하는 값들만 생각한다. y=1인 경우에 f(x) = 1이므로 이 때 cost가 0으로 가게 된다.
그리고 실제로는 y=1일 때 f(x) = 0으로 가게 되면 패널티를 줘야한다.
그래서 x값이 0으로 갈수록 큰 값의 cost를 주는 식으로 설계한다.
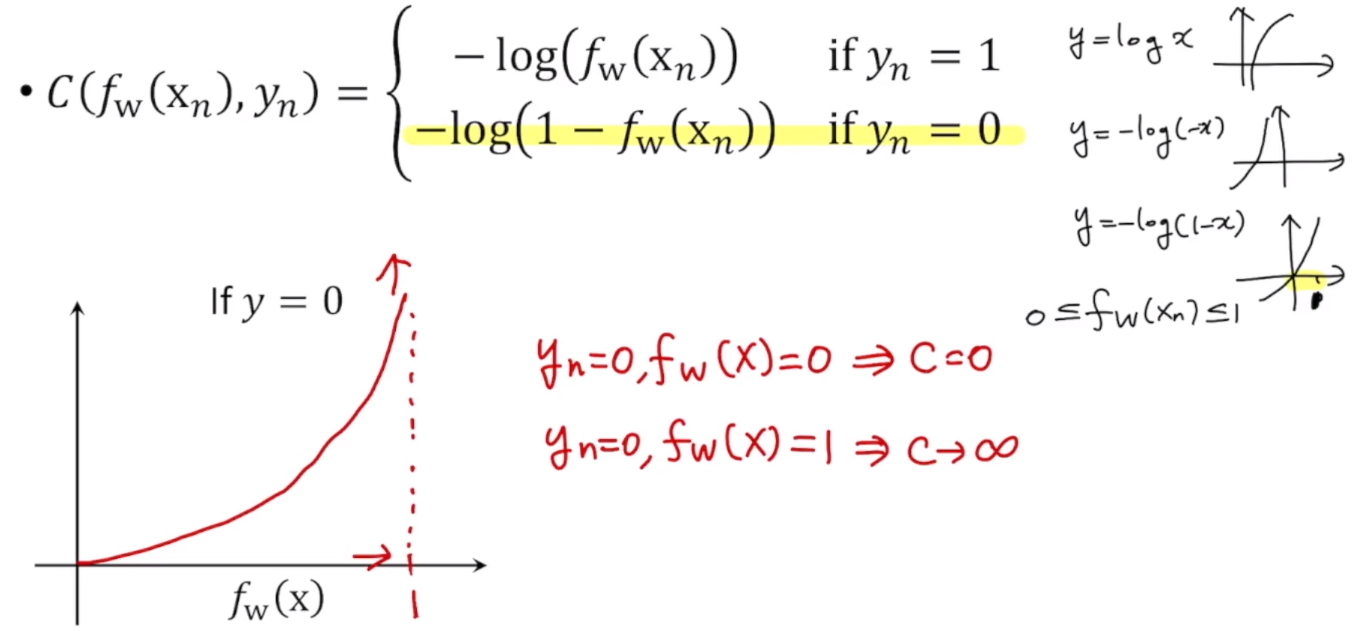
fw(x) 는 항상 0에서 1사이의 값만 생각을 하기 때문에, 이 범위 안에 있는 그래프를 그려줬다.
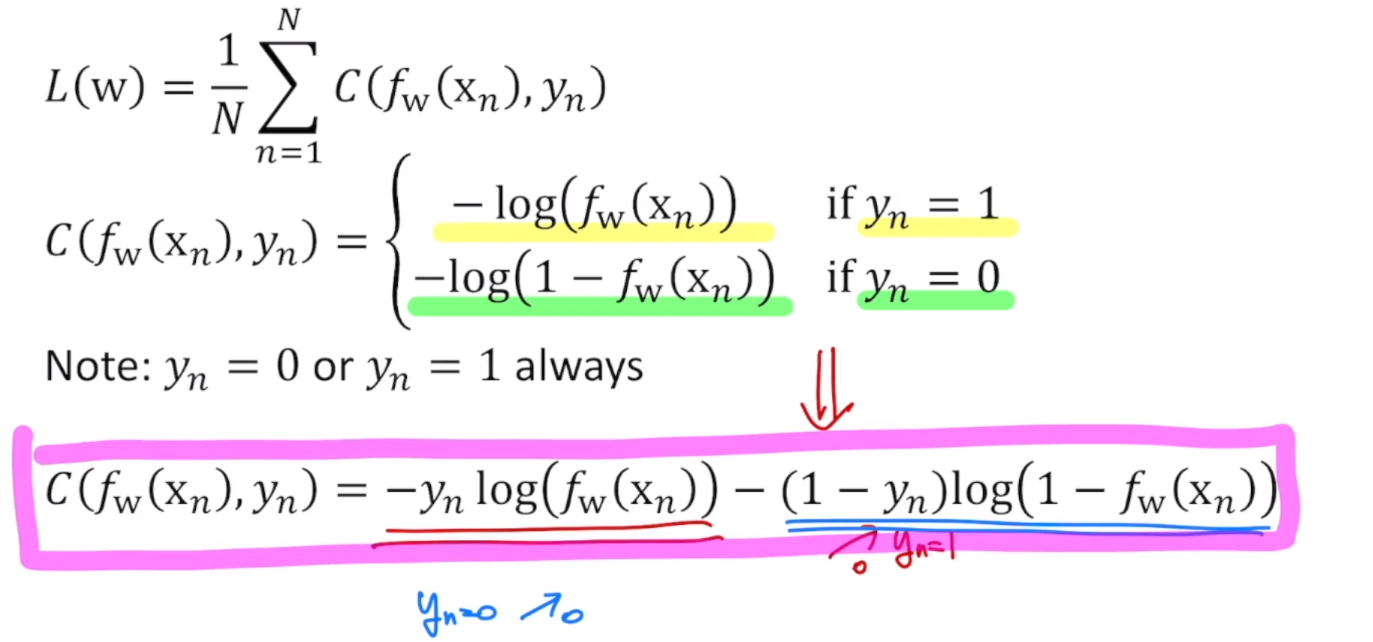
yn=1일 때의 식과 yn=0일 때의 식을 합쳐서 다음과 같이 c(fw(xn), yn)을 나타낼 수 있다. yn=1일 때는 오른쪽 부분이 사라지고 왼쪽 부분만 남게되고, yn=0일 때는 왼쪽 부분만 남고 오른쪽 부분은 사라진다.

이런 비용함수를 minimization하는 w를 찾음으로써, 적합한 파라미터를 찾을 수 있다. 이렇게 파라미터를 찾았기 때문에 f(x)를 구할 수 있고, 새로운 x에 대해서 위의 마지막 식을 통해 어떤 값을 prediction할 수 있다.
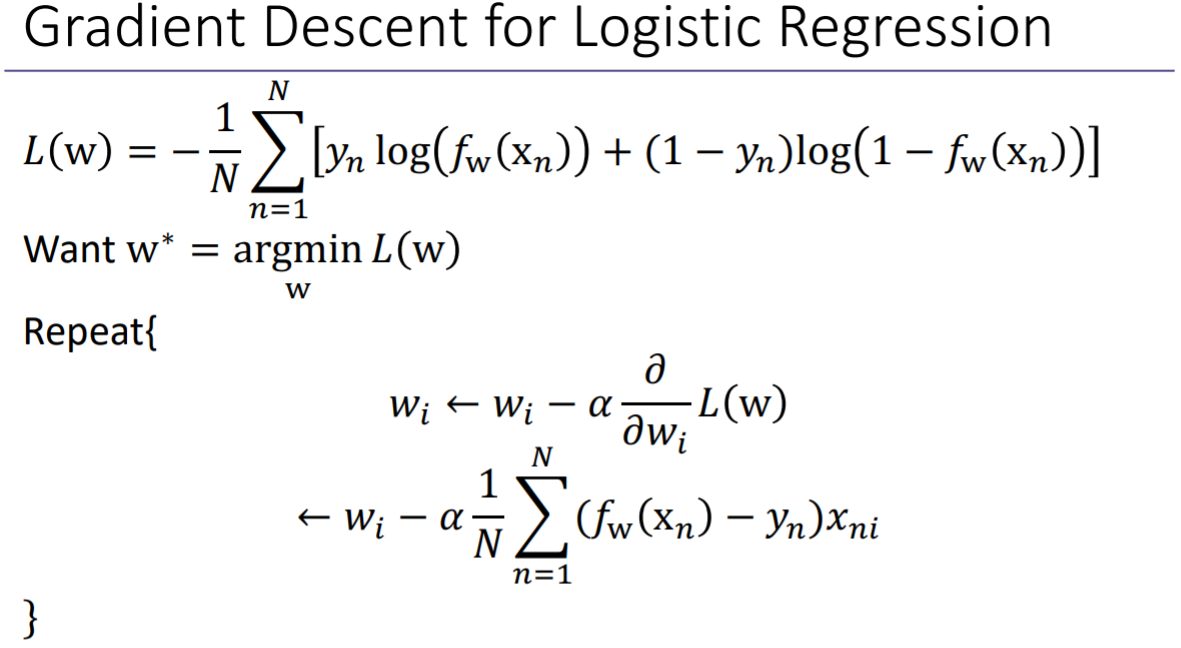
앞에서 logistic regression에 대해서 MSE를 사용할 때, w에 대해서 미분을 하면, non-convex한 값을 갖게돼서 gradient descent 방법을 사용할 수 없다고 했었다.
하지만 위와 같은 식을 사용하게 되면, convex한 형태가 되기 때문에 코스트 함수를 이렇게 정의하면 gradient descent 방법을 사용해서 w를 구할 수 있다.
linear regression에서 수행했던 것과 마찬가지로 각 wi에 대해서 코스트 함수를 미분해서, 적절한 learning rate를 곱하고 negative 방향의 gradient를 계속해서 빼주어서 파라미터를 업데이트할 수 있다. 이렇게 계속 반복하여 계산해서 수렴할때까지 반복하면 global minimum까지 도달하게 된다.
지금까지는 0또는 1의 binary classification에 대해서 살펴봤다. 근데 만약 binary 형태의 데이터가 아니라 Multi-class라면 어떻게 될까?
binary일 경우에는, 이메일을 스팸이냐 또는 스팸이 아니냐, 이렇게 0또는 1. 2가지의 케이스에 대해서 생각했지만, 이제부터는 그 이메일이 직장과 관련된건지, 친구들과 관련된건지, 가족과 관련한건지 또는 취미와 관련한건지 하는 이런 식으로 이메일을 tagging이 가능하다. → 이 때는 클래스가 4개임
⇒ 기존의 바이너리 classification에서 클래스를 확장시킴
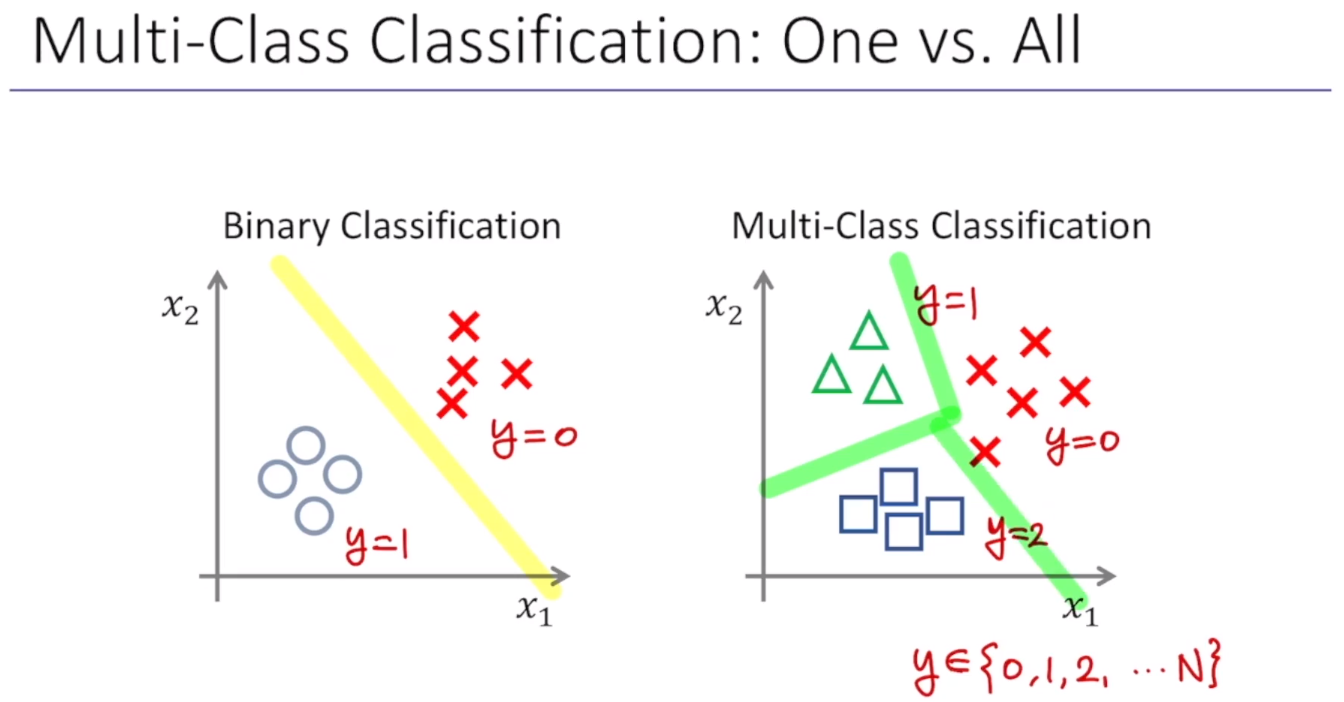
Binary Classification은 y가 0또는1. 이렇게 2가지의 경우뿐이다. 반면 Multi-Class Classification은 y=0. 1. 2 등등.. 으로 n개의 값을 갖는 클래스를 갖는 경우이다. 그리고 각각의 decision boundary가 표시되어있다.
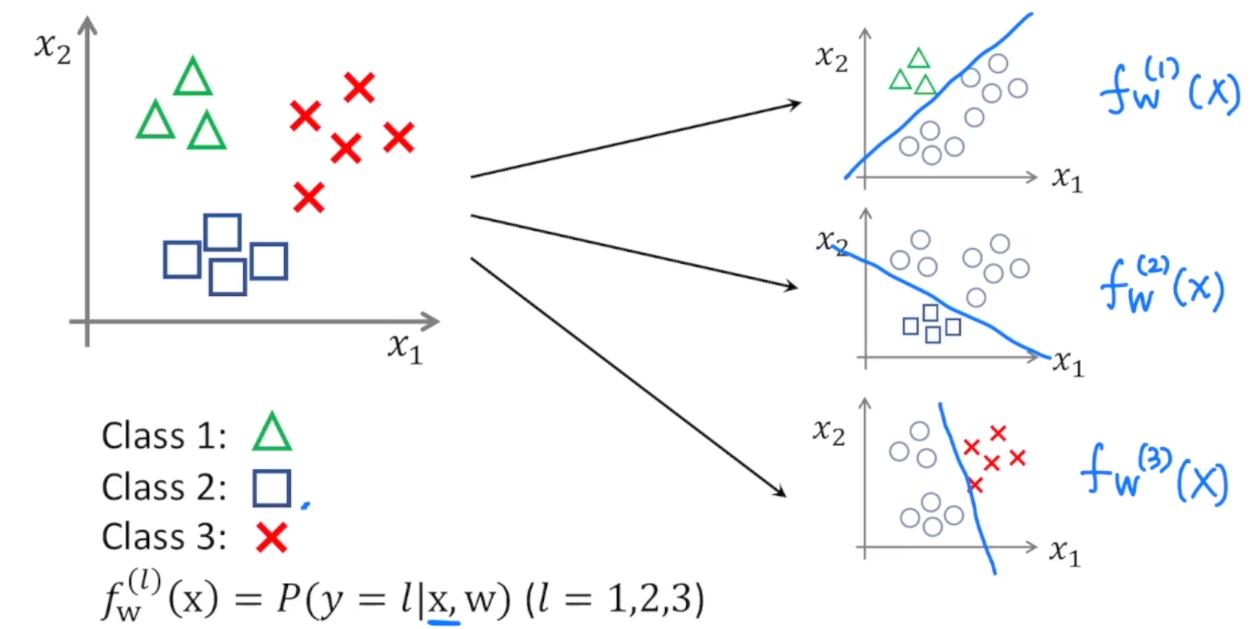
Multi-Class를 갖는 데이터들을 classification하기 위해서는, 다음과 같이 각각에 대해서 decision boundary를 구함으로써 매핑 함수를 구해서 풀 수 있다.
Class 1의 경우는 세모를 데이터들과 구분하고 싶은 것이기 때문에, decision boundary를 위와 같이 설정해서 매핑함수 fx(1)(x)를 찾았다. 마찬가지로 Class 2와 Class 3에 대해서도 decision boundary를 설정하고 매핑 함수를 찾는다.
그래서 여기에서 매핑 함수는 어떤 파라미터들을 이용해서 정의가 된 x들이 있을 때, y가 각각 1, 2, 3일 경우가 된다.

Multi-Class classification에서는, 각각의 클래스에 대해 서로 다른 logistic classification을 수행해서 어떤 y=l일때의 probabiliy를 구할 수 있다. 새로운 x에 대해서는 각각 probabiliy를 구해서, 그 값이 가장 큰 레이블 l을 선택하면, 그것이 x에 대한 prediction이 된다.
'전공 > 컴퓨터 비전' 카테고리의 다른 글
| [컴퓨터 비전] Introduction to Deep Learning (0) | 2021.04.20 |
|---|---|
| [컴퓨터 비전] Neural Networks and Backpropagation (0) | 2021.04.18 |
| [컴퓨터 비전] Introduction to Image Processing (2) | 2021.04.07 |
